【物理】座標変換と慣性力(コリオリ力・遠心力)【力学】

今回は座標変換と慣性力について考えていきます。

観測者によって質点の運動の軌跡が違って見えることがあります。

例えば電車の中でボールを投げた場合、電車の中にいる人からみたボールの軌跡と電車の外にいる人からみたボールの軌跡は異なっています。

そして、観測者によって本来質点に加わっている力の他に、本来質点に加わっていないみかけの力がはたらいているように見えます。

このような見かけの力のことを慣性力といいます。

様々な座標変換を通して、慣性力について考えていきます。

今回の記事では

• 慣性系の座標変換
• ガリレイ変換
• 慣性力
• 回転座標系とコリオリ力・遠心力

について解説していきます。

慣性系の座標変換

慣性系とは何も力を受けていない質点が等速度運動する系のことであり、ニュートンの第1法則が成り立つ系です。

運動の記述に用いられる座標系の取り方は基本的には慣性系を用いた方がよいです。

それは例えば時間変化するような座標系を用いた場合、質点の運動が複雑な式で表されてしまい、本来知りたい質点の運動の様子が分かりにくくなってしまうからです。

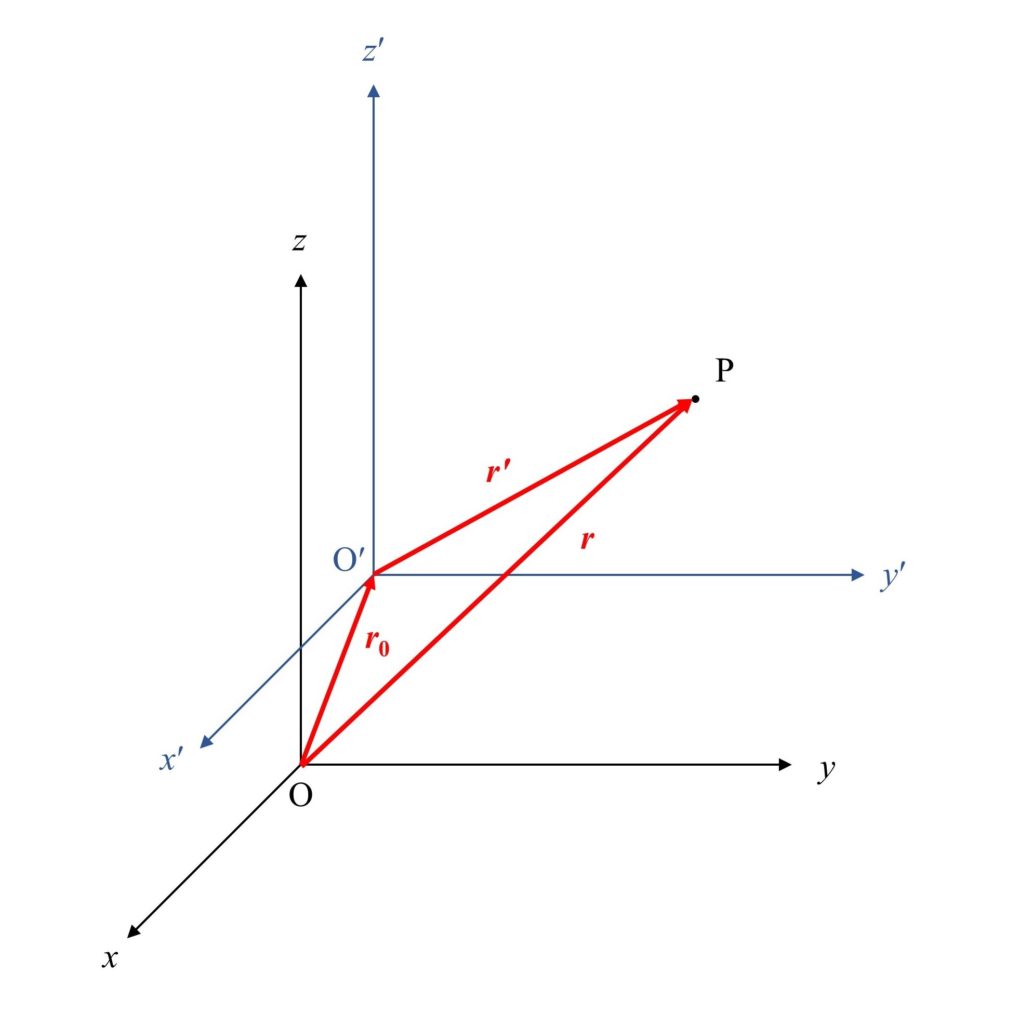
いま、慣性系となる座標系を${\rm O}-xyz$とし、$x$軸、$y$軸、$z$軸に対してそれぞれ平行に$x’$軸、$y’$軸、$z’$軸をとり、原点を$\rm O’$とした座標系を${\rm O’}-x’y’z’$とします。

点$\rm O’$の位置を${\rm O}-xyz$系から見ると、

\begin{eqnarray}
{\rm{O}}'(x_0(t),y_0(t),z_0(t))\tag{1}
\end{eqnarray}

のように運動している座標系と考えます。このとき質点$\rm P$の位置は、

\begin{eqnarray}
x=x_0+x’,y=y_0+y’,z=z_0+z’\tag{2}
\end{eqnarray}

が成り立ち、ベクトル表記で書くと、

\begin{eqnarray}
\boldsymbol{r}=\boldsymbol{r_0}+\boldsymbol{r’}\tag{3}
\end{eqnarray}

となります。ここまでをまとめると下図のようになります。

位置を$t$で微分すると、

\begin{eqnarray}
\dot{x}=\dot{x}_0+\dot{x}’,\dot{y}=\dot{y}_0+\dot{y}’,\dot{z}=\dot{z}_0+\dot{z}’\tag{4}
\end{eqnarray}

となり、ベクトル表記では、

\begin{eqnarray}
\boldsymbol{\dot{r}}=\boldsymbol{\dot{r}_0}+\boldsymbol{\dot{r}’}\tag{5}
\end{eqnarray}

となります。さらに$t$で微分すると、

\begin{eqnarray}
\ddot{x}=\ddot{x}_0+\ddot{x}’,\ddot{y}=\ddot{y}_0+\ddot{y}’,\ddot{z}=\ddot{z}_0+\ddot{z}’\tag{6}
\end{eqnarray}

となり、ベクトル表記では、

\begin{eqnarray}
\boldsymbol{\ddot{r}}=\boldsymbol{\ddot{r}_0}+\boldsymbol{\ddot{r}’}\tag{7}
\end{eqnarray}

となります。今、${\rm O}-xyz$系から見た場合慣性系としているのでニュートンの第2法則が成り立ち、質点の質量を$m$、質点にはたらく力を$\boldsymbol{F}$とすると、運動方程式$\boldsymbol{F}=m\boldsymbol{\ddot{r}}$が成り立ちます。すなわち、

\begin{eqnarray}
\boldsymbol{F}&=&m\boldsymbol{\ddot{r}}\\
&=&m(\boldsymbol{\ddot{r}_0}+\boldsymbol{\ddot{r}’})\tag{8}
\end{eqnarray}

となります。位置については原点の取り方によって座標が変化するので、質点の位置ベクトルは${\rm O}-xyz$系と${\rm O’}-x’y’z’$系で異なります。

だから位置ベクトル$\boldsymbol{r}$と$\boldsymbol{r’}$は明確に区別する必要があります。

一方で質点にはたらく力は座標系が変わっても変化しません。

つまり、${\rm O}-xyz$系でも${\rm O’}-x’y’z’$系でも質点$\rm P$にはたらく力は$\boldsymbol{F}$となります。

座標系の相対速度$\boldsymbol{\dot{r}_0}$が時間によらない(一定)とすれば、$\boldsymbol{\ddot{r}_0}=0$となるので、

\begin{eqnarray}
\boldsymbol{F}&=&m(\boldsymbol{\ddot{r}_0}+\boldsymbol{\ddot{r}’})r\\
&=&m\boldsymbol{\ddot{r}’}\tag{9}
\end{eqnarray}

となり、${\rm O’}-x’y’z’$系でも力と加速度が比例します。

つまり${\rm O’}-x’y’z’$系でも$\boldsymbol{F}=0$ならば、$\boldsymbol{\ddot{r}’}=0$となるので$\boldsymbol{\dot{r}’}=$一定となり、運動の第1法則が成り立ち、${\rm O’}-x’y’z’$系も慣性系であることがわかります。

以上より、慣性系${\rm O}-xyz$系に対して相対速度$\boldsymbol{\ddot{r}’}=0$が一定である座標系${\rm O’}-x’y’z’$系を取った場合には、${\rm O’}-x’y’z’$は慣性系となります。

つまり、ある慣性系に対して等速度で動く座標系は慣性系となります。

慣性力

もし$\boldsymbol{\ddot{r}_0}\neq0$ならば式(8)より、

\begin{eqnarray}
m\boldsymbol{\ddot{r}’}&=&\boldsymbol{F}-m\boldsymbol{\ddot{r}_0}\tag{10}
\end{eqnarray}

となり、${\rm O’}-x’y’z’$系に静止した観測者からすると、本来質点に加わっている$\boldsymbol{F}$のほかにみかけの力$-m\boldsymbol{\ddot{r}_0}$が加わっているように見えます。

このようなみかけの力を「慣性力」といいます。

このようにみかけの力をつけくわえなければニュートンの運動法則が成り立たないような系は慣性系ではないです。

ガリレイ変換

さて、相対速度が一定のときの速度を$\boldsymbol{\dot{r}_0}\equiv \boldsymbol{v}_0$とすると式(5)は、

\begin{eqnarray}
\boldsymbol{\dot{r}}=\boldsymbol{v}_0+\boldsymbol{\dot{r}’}\tag{11}
\end{eqnarray}

となります。シンプルに考えるために$\boldsymbol{v}_0$は$x$軸($x’$軸)方向であるとします。

すると、${\rm O}-xyz$系と${\rm O’}-x’y’z’$系の速度の関係は、

\begin{eqnarray}
\dot{x}=v_0+\dot{x}’,\dot{y}=\dot{y}’,\dot{z}=\dot{z}’\tag{12}
\end{eqnarray}

となります。式(11)を$t$で積分することで位置の関係を導くことができ、点$\rm O$と点$\rm O’$が一致するときの時刻を$t=0$とすると、

\begin{eqnarray}
x=v_0t+x’,y=y’,z=z’\tag{13}
\end{eqnarray}

となります。以上より${\rm O}-xyz$系と${\rm O’}-x’y’z’$系の位置が関連づけられました。

式(11)の座標変換を「ガリレイ変換」と呼びます。

回転座標系

つづいて2次元平面において慣性系に対して一定の角速度で回転するような座標系を考えます。

どちらの座標系においても原点を$\rm O$に固定し、時刻$t=0$のときに$x$軸と$x’$軸が一致し、$y$軸と$y’$軸が一致するとします。

$x’$軸$y’$軸を回転座標系として慣性系に対して角速度$\omega$で回転するとします。

また質点Pを慣性系からみたときの座標を$(x,y)$、回転座標系からみたときの座標を$(x’,y’)$とします。

両座標系の関係は下図のようになります。

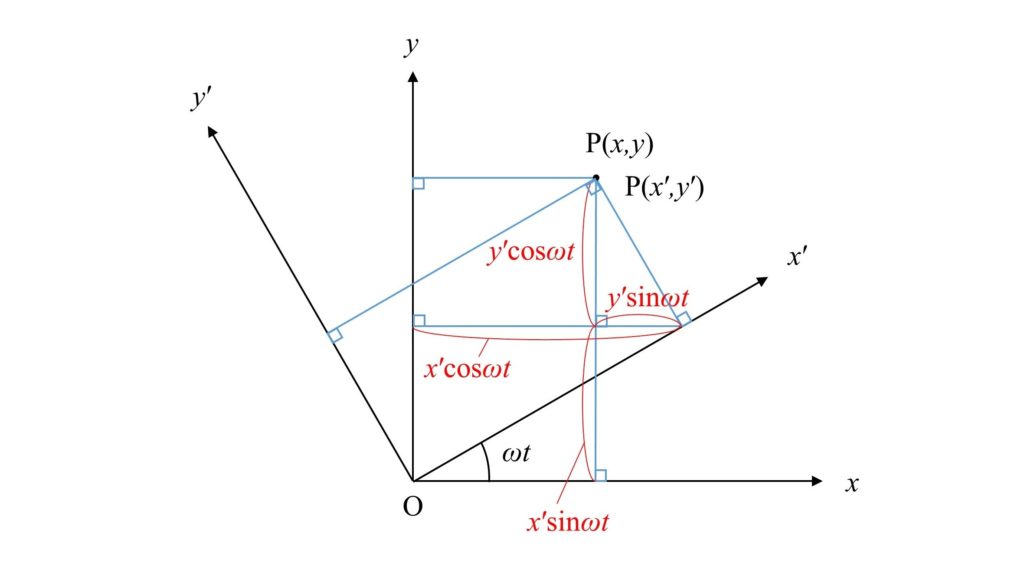
上図により$(x,y)$と$(x’,y’)$は、

\begin{eqnarray}
x=x’\cos\omega t-y’\sin\omega t\tag{14}\\
y=x’\sin\omega t+y’\cos\omega t\tag{15}
\end{eqnarray}

と変換することができます。$t$で微分すると、

\begin{eqnarray}
\dot{x}=\dot{x}’\cos\omega t-\omega x’\sin\omega t-\dot{y}’\sin\omega t-\omega y’\cos\omega t\tag{16}\\
\dot{y}=\dot{x}’\sin\omega t+\omega x’\cos\omega t+\dot{y}’\cos\omega t-\omega y’\sin\omega t\tag{17}
\end{eqnarray}

となり、さらに$t$で微分すると、

\begin{eqnarray}
\ddot{x}&=&\ddot{x}’\cos\omega t-\omega \dot{x}’\sin\omega t-\omega \dot{x}’\sin\omega t-\omega^2 x’\cos\omega t\\
&&-\ddot{y}’\sin\omega t-\omega\dot{y}’\cos\omega t-\omega \dot{y}’\cos\omega t+\omega^2 y’\sin\omega t\\
&=&(\ddot{x}’-\omega^2 x’-\omega\dot{y}’-\omega \dot{y}’)\cos\omega t-(\omega \dot{x}’+\omega \dot{x}’+\ddot{y}’-\omega^2 y’)\sin\omega t\\
&=&(\ddot{x}’-2\omega\dot{y}’-\omega^2 x’)\cos\omega t-(\ddot{y}’+2\omega \dot{x}’-\omega^2 y’)\sin\omega t\tag{18}\\
\ddot{y}&=&\ddot{x}’\sin\omega t+\omega\dot{x}’\cos\omega t+\omega \dot{x}’\cos\omega t-\omega^2 x’\sin\omega t\\
&&+\ddot{y}’\cos\omega t-\omega\dot{y}’\sin\omega t-\omega \dot{y}’\sin\omega t-\omega^2 y’\cos\omega t\\
&=&(\ddot{x}’-\omega^2 x’-\omega\dot{y}’-\omega \dot{y}’)\sin\omega t+(\omega \dot{x}’+\omega \dot{x}’+\ddot{y}’-\omega^2 y’)\cos\omega t\\
&=&(\ddot{x}’-2\omega\dot{y}’-\omega^2 x’)\sin\omega t+(\ddot{y}’+2\omega \dot{x}’-\omega^2 y’)\cos\omega t\tag{19}
\end{eqnarray}

となります。ここで加速度成分の関係式は、

\begin{eqnarray}
A_x&=&A_{x’}\cos\omega t-A_{y’}\sin\omega t\tag{20}\\
A_y&=&A_{x’}\sin\omega t+A_{y’}\cos\omega t\tag{21}
\end{eqnarray}

であり、式(18)と式(20)、式(19)と式(21)の成分を比較して、

\begin{eqnarray}
A_{x’}&=&\ddot{x}’-2\omega\dot{y}’-\omega^2 x’\tag{22}\\
A_{y’}&=&\ddot{y}’+2\omega\dot{x}’-\omega^2 y’\tag{23}
\end{eqnarray}

となります。回転座標系における運動運動方程式は、

\begin{eqnarray}
mA_{x’}&=&F_{x’}\tag{24}\\
mA_{y’}&=&F_{y’}\tag{25}
\end{eqnarray}

なので、式(24)(25)に式(22)(23)を代入すると、

\begin{eqnarray}
m(\ddot{x}’-2\omega\dot{y}’-\omega^2 x’)&=&F_{x’}\tag{26}\\
m(\ddot{y}’+2\omega\dot{x}’-\omega^2 y’)&=&F_{y’}\tag{27}
\end{eqnarray}

となるので式を整理すると、

\begin{eqnarray}
m\ddot{x}’&=&F_{x’}+2m\omega\dot{y}’+m\omega^2 x’\tag{28}\\
m\ddot{y}’&=&F_{y’}-2m\omega\dot{x}’+m\omega^2 y’\tag{29}
\end{eqnarray}

となります。実際に質点Pにはたらいている力は回転座標系において$F_{x’},F_{y’}$ですが、回転により2種類(右辺第2項・第3項)の慣性力がはたらいていることがわかります。

右辺第2項：コリオリ力、第3項：遠心力を表しています。

コリオリ力・遠心力

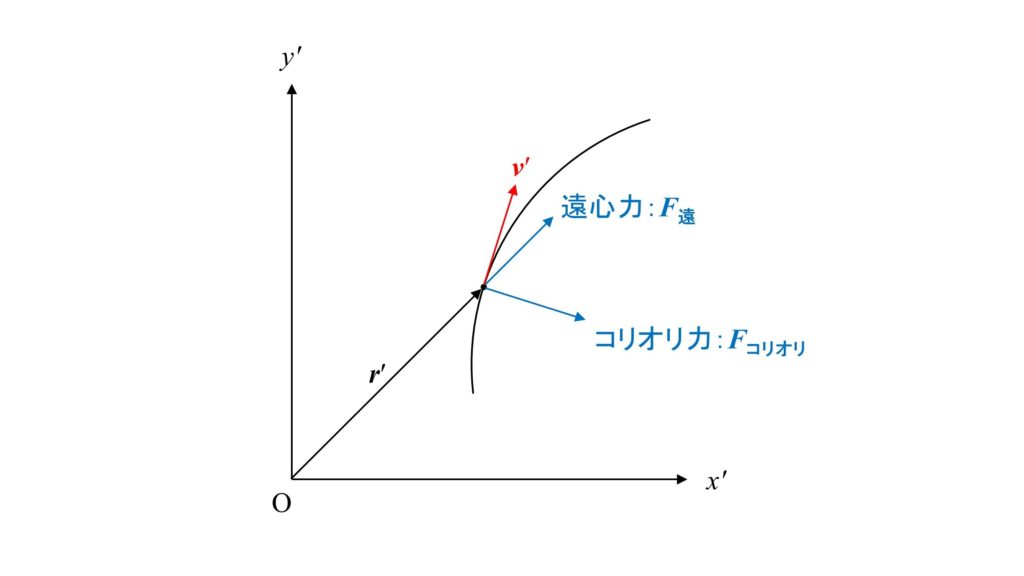
回転座標系から見た質点の位置$\boldsymbol{r}’=(x’,y’)$、速度$\boldsymbol{v}’=(\dot{x}’,\dot{y}’)$、コリオリ力$\boldsymbol{F}_{コリオリ}=(2m\omega\dot{y}’,-2m\omega\dot{x}’)$、遠心力$\boldsymbol{F}_{遠}=(m\omega^2 x’,m\omega^2 y’)$とします。

コリオリ力の大きさ$|\boldsymbol{F}_{コリオリ}|$は、

\begin{eqnarray}
|\boldsymbol{F}_{コリオリ}|&=&\sqrt{(2m\omega\dot{y}’)^2+(-2m\omega\dot{x}’)^2}\\
&=&2m\omega\sqrt{\dot{y}’^2+\dot{x}’^2}\\
&=&2m\omega|\boldsymbol{v}’|\tag{30}
\end{eqnarray}

となり、コリオリ力は速度に比例して大きくなります。

コリオリ力$\boldsymbol{F}_{コリオリ}$と速度$\boldsymbol{v}’$の内積は、

\begin{eqnarray}
\boldsymbol{F}_{コリオリ}\cdot\boldsymbol{v}’=2m\omega\dot{x}’\dot{y}’-2m\omega\dot{x}’\dot{y}’=0\tag{31}
\end{eqnarray}

となるので、コリオリ力と速度のベクトルは垂直に交わることがわかります。

回転軸方向を向き、大きさが角速度$\omega$のような角速度ベクトル$\boldsymbol{\omega}$とすると、コリオリ力$\boldsymbol{F}_{コリオリ}=-2m\boldsymbol{\omega}×\boldsymbol{v’}$と表すこともできます。

第3項の遠心力は$\boldsymbol{F}_{遠}=m\omega^2\boldsymbol{r}’$と表すことができます。

回転座標系から見た場合、コリオリ力・遠心力は下図のようにはたらきます。

最後に

２つの座標系を設定し、慣性系同士の座標変換・平行移動する座標系の座標変換・慣性系と回転座標系の座標変換について考えていきました。

座標変換を通して、コリオリ力や遠心力といった慣性力についても考えていきました。

観測者によって慣性力というみかけの力が加わっているように見えるのは不思議に思えるかもしれませんが、電車の中と外の人からみたときのものの運動の様子の違いやメリーゴーランドに乗っている人と外で立っている人からみたものの運動の様子を考えてみるとイメージしやすくなるかもしれません。

Baby steps to Giant Strides!