【物理】運動方程式(速度に比例する抵抗がある場合の落下運動)【力学】

前回は運動法方程式について学び、具体例として自由落下運動と放物運動を用いて運動方程式の解き方について解説しました。

前回自由落下運動について運動方程式を解いたときに説明しましたが、運動を数式で理解するためには以下のプロセスで計算を行っていきます。

(1)成分ごとに運動方程式を立てる。
(2)微分方程式を解く。
(3)初期条件を代入し、位置や速度を $t$ の関数で表す。

これによって運動方程式を解き、物体の運動を予測することができます。

今回も運動方程式が主たるテーマとなりますが、速度に比例する抵抗があるときの運動について運動方程式を書き、微分方程式を解いていきます。

Contents

速度に比例する抵抗がある場合の落下運動
最後に

速度に比例する抵抗がある場合の落下運動

速度に比例する抵抗がある場合の落下運動について考えていきます。

(1)成分ごとに運動方程式を立てる

鉛直上向きを正として$y$ 軸をとります。成分ごとに運動方程式を立てていくのですが、今回は落下運動なので $y$ 軸方向のみの運動方程式を立てることになります。

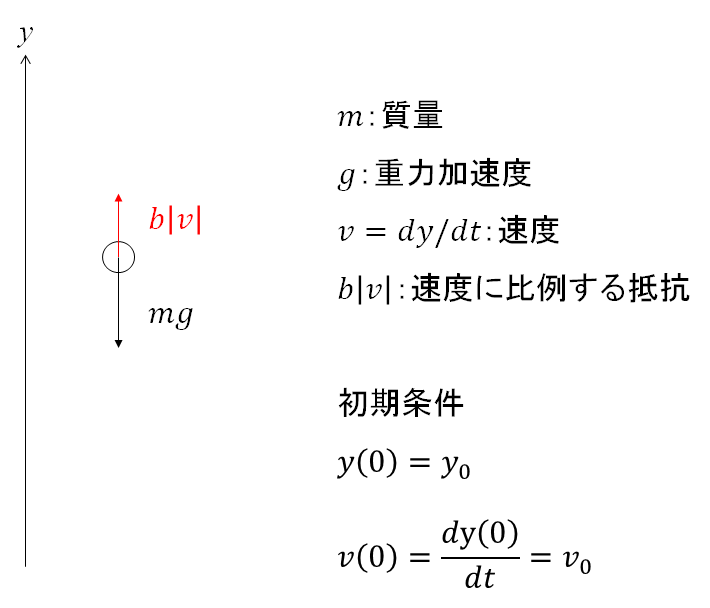
地上の物体は全て鉛直下向き(今の設定でいうならば $y$ の負方向)に大きさ $mg$ の力を受けます。$m$ は質量、$g$ は重力加速度です。

また、速度に比例する抵抗は $b$ を定数として $b|v|$ と表すことができます。ただし速度 $v=\frac{dy}{dt}$、 $b＞0$ です。

初期条件(時間 $t=0$ のときの条件)として位置 $y(0)=y_0$、初速度 $v(0)=v_0$ とします。

ここまでの条件を図でまとめておきます。

ここで少し $v$ の符号について考えます。
今、位置について鉛直上向きを正としています。そして落下運動を考えているので、位置は鉛直下向きに移動していきます。

つまり $v=\frac{dy}{dt}<0$ となり、$|v|=-v$ となります。
だから速度に比例する抵抗の大きさは $b|v|=-bv$ となります。

ここまでの条件から、速度に比例する抵抗がある場合の落下運動における運動方程式は以下のようになります。

$$
\begin{align}
m\frac{dv}{dt}&=-bv-mg\tag{1}
\end{align}
$$

(2)微分方程式を解く

さて、それではこの微分方程式を解いていきましょう。

まず両辺を $m$ で割ります。

$$
\begin{align}
\frac{dv}{dt}&=-\frac{b}{m}v-g\\
&=-\frac{b}{m}(v+\frac{mg}{b})\tag{2}
\end{align}
$$

ここで $V=v+\frac{mg}{b}$ とおきます。この両辺を $t$ で微分すると次のようになります。

$$
\begin{align}
\frac{dV}{dt}=\frac{dv}{dt}
\end{align}
$$

よって式(2)は次のようになります。

$$
\begin{align}
\frac{dV}{dt}=-\frac{b}{m}V\tag{3}
\end{align}
$$

これで式がかなりシンプルな形になったと思います。

式(3)を変数分離で解いていきます。式(3)の左辺を $V$、右辺を $t$ を集めると次のようになります。

$$
\begin{align}
\frac{dV}{V}=-\frac{b}{m}dt\tag{4}
\end{align}
$$

続いて式(4)の両辺を積分してきます。

$$
\begin{align}
\int\frac{dV}{V}&=-\frac{b}{m}\int dt\\
\ln|V|&=-\frac{b}{m}t+C’
\end{align}
$$
$C’$ は積分定数です。

式中に $\ln$ とありますが、これは自然対数のことで、 $e$ を底とする対数のことです。つまり $\ln x=\log_ex$ と書き換えられます。

さて、続けて解いていきましょう。

$$
\begin{align}
\ln|V|&=-\frac{b}{m}t+C’\\
|V|&=e^{-\frac{b}{m}t+C’}\\
&=e^{C’}e^{-\frac{b}{m}t}\tag{5}
\end{align}
$$

ここで $C’$ は定数なので $e^{C’}$ も定数となります。だから微分方程式を解く上で $e^{C’}$ をある積分定数 $C$とおいても不都合はありません。

そこで式(5)を次のように書き換えます。

$$
\begin{align}
|V|&=Ce^{-\frac{b}{m}t}\tag{6}
\end{align}
$$

さらに $V$ の符号についても定数 $C$ に押しつけることができます。

そこで式(6)は次のようにしても解くことができます。

$$
\begin{align}
V&=Ce^{-\frac{b}{m}t}\tag{7}
\end{align}
$$

さて微分方程式を解く最初のあたりで $V=v+\frac{mg}{b}$ としていたので、式(7)を代入することで $v$ を求めることができます。

$$
\begin{align}
v&=V-\frac{mg}{b}\\
\\
&\Downarrow V=Ce^{-\frac{b}{m}t}代入\\
\\
v&=Ce^{-\frac{b}{m}t}-\frac{mg}{b}\tag{8}
\end{align}
$$

また速度 $v=\frac{dy}{dt}$ なので、式(8)の両辺を積分することで、位置 $y$ を表す式を導くことができます。

$$
\begin{align}
v&=Ce^{-\frac{b}{m}t}-\frac{mg}{b}\\
\\
&\Downarrow v=\frac{dy}{dt}\\
\\
\frac{dy}{dt}&=Ce^{-\frac{b}{m}t}-\frac{mg}{b}\\
\\
&\Downarrow 変数分離して積分\\
\\
\int dy&=\int (Ce^{-\frac{b}{m}t}-\frac{mg}{b})dt\\
\\
&\Downarrow 計算\\
\\
y&=-\frac{m}{b}Ce^{-\frac{b}{m}t}-\frac{mg}{b}t+D\tag{9}
\end{align}
$$
$D$ は積分定数です。

さて、ここまでで積分定数を含む形で式(8)(9)のように位置 $y$ と速度 $v$ を求めることができした。

$$
\begin{align}
v&=Ce^{-\frac{b}{m}t}-\frac{mg}{b}\tag{8}\\
y&=-\frac{m}{b}Ce^{-\frac{b}{m}t}-\frac{mg}{b}t+D\tag{9}
\end{align}
$$
$C,D$ は積分定数

(3)初期条件を代入し、位置や速度を $t$ の関数で表す

続いては初期条件を代入して $C,D$ を求めていきます。初期条件(時間 $t=0$ のときの条件)は位置 $y(0)=y_0$、初速度 $v(0)=v_0$ です。

まずは式(8)に $t=0, v=v_0$ を代入して $C$ を求めていきます。

$$
\begin{align}
v&=Ce^{-\frac{b}{m}t}-\frac{mg}{b}\\
\\
&\Downarrow t=0, v=v_0\\
\\
v_0&=Ce^0-\frac{mg}{b}\\
\\
&\Downarrow 移項\\
\\
C&=v_0+\frac{mg}{b}
\end{align}
$$

続いて式(9)に $t=0, y=y_0, C=v_0+\frac{mg}{b}$ を代入して $D$ を求めます。

$$
\begin{align}
y&=-\frac{m}{b}Ce^{-\frac{b}{m}t}-\frac{mg}{b}t+D\\
\\
&\Downarrow t=0, y=y_0, C=v_0+\frac{mg}{b}\\
\\
y_0&=-\frac{m}{b}(v_0+\frac{mg}{b})e^0-\frac{mg}{b}\cdot0+D\\
\\
&\Downarrow 移項\\
\\
D&=y_0+\frac{m}{b}(v_0+\frac{mg}{b})e^0+\frac{mg}{b}\cdot0\\
\\
&\Downarrow 計算\\
\\
D&=y_0+\frac{m}{b}(v_0+\frac{mg}{b})
\end{align}
$$

これで $C,D$ を求めることができました。最後に $C,D$ を式(8)(9)に代入して位置 $y$ と速度 $v$ を求めます。

まず式(8)に先ほど求めた $C=v_0+\frac{mg}{b}$ を代入して $v$ を求めます。

$$
\begin{align}
v&=Ce^{-\frac{b}{m}t}-\frac{mg}{b}\\
\\
&\Downarrow C=v_0+\frac{mg}{b}\\
\\
v&=(v_0+\frac{mg}{b})e^{-\frac{b}{m}t}-\frac{mg}{b}
\end{align}
$$

続いて式(9)に先ほど求めた $C=v_0+\frac{mg}{b},D=y_0+\frac{m}{b}(v_0+\frac{mg}{b})$ を代入して $y$ を求めます。

$$
\begin{align}
y&=-\frac{m}{b}Ce^{-\frac{b}{m}t}-\frac{mg}{b}t+D\\
\\
&\Downarrow C=v_0+\frac{mg}{b},D=y_0+\frac{m}{b}(v_0+\frac{mg}{b})\\
\\
y&=-\frac{m}{b}(v_0+\frac{mg}{b})e^{-\frac{b}{m}t}-\frac{mg}{b}t+y_0+\frac{m}{b}(v_0+\frac{mg}{b})\\
\\
&\Downarrow 式を整理\\
\\
y&=y_0-\frac{mg}{b}t+\frac{m}{b}(v_0+\frac{mg}{b})(1-e^{-\frac{b}{m}t})
\end{align}
$$

以上で位置 $y$ と速度 $v$ を $t$ の式で表すことができました。

$$
\begin{align}
y&=y_0-\frac{mg}{b}t+\frac{m}{b}(v_0+\frac{mg}{b})(1-e^{-\frac{b}{m}t})\\
v&=(v_0+\frac{mg}{b})e^{-\frac{b}{m}t}-\frac{mg}{b}
\end{align}
$$

さて、ここで速度 $v$ について注目してみましょう。速度 $v$ は初速度は $v_0$ ですが、時間が立つとどのように速度は変化するでしょうか？

$t\rightarrow\infty$ のとき $e^{-\frac{b}{m}t}\rightarrow0$ となります。つまり$t\rightarrow\infty$ の極限をとると $v$ は次のようになります。

$$
\begin{align}
\lim_{t\rightarrow\infty} v=-\frac{mg}{b}
\end{align}
$$

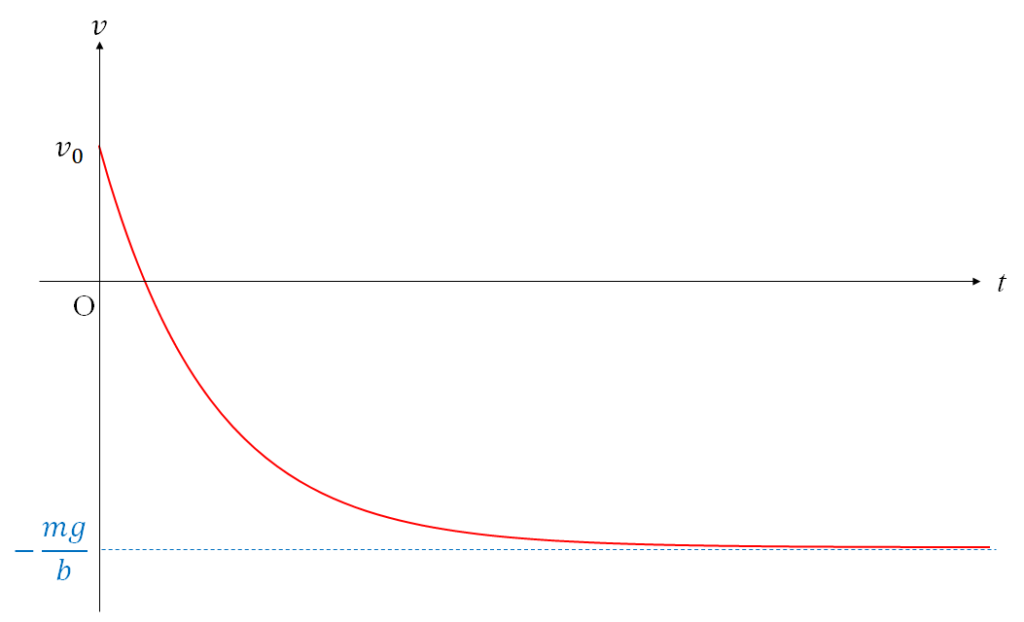
つまり、速度に比例する抵抗がある場合、速度 $v$ は十分に時間が経過すると $v=-\frac{mg}{b}$ の一定速度になることがわかります。

以下に速度に比例する抵抗があるときの落下運動における速度の時間変化のグラフを示しておきます。