前回は速度に比例する抵抗があるときの運動について学びました。今回は速度の2乗に比例する抵抗があるときの落下運動について考えていきます。
これまでと同様に、以下の手順で速度の2乗に比例する抵抗があるときの落下運動について理解を深めていきます。
(1)成分ごとに運動方程式を立てる。
(2)微分方程式を解く。
(3)初期条件を代入し、位置や速度を \(t\) の関数で表す。
これによって運動方程式を解き、物体の運動を予測することができます。
速度の2乗に比例する抵抗がある場合の落下運動
速度の2乗に比例する抵抗がある場合の落下運動について考えていきます。
(1)成分ごとに運動方程式を立てる
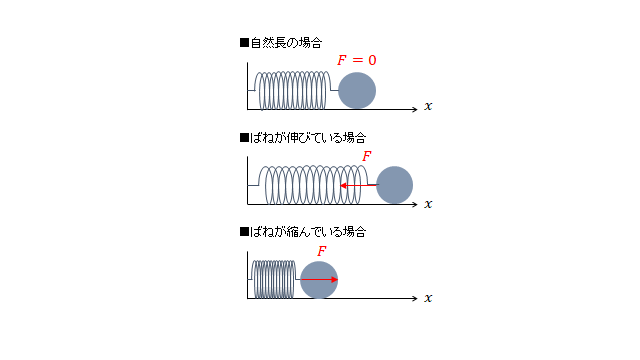
鉛直上向きを正として \(y\) 軸をとります。成分ごとに運動方程式を立てていくのですが、今回は落下運動なので \(y\) 軸方向のみの運動方程式を立てることになります。
地上の物体は全て鉛直下向き(今の設定でいうならば \(y\) の負方向)に大きさ \(mg\) の力を受けます。\(m\) は質量、\(g\) は重力加速度です。
また、速度に比例する抵抗は \(k\) を定数として \(kv^2\) と表すことができます。ただし速度 \(v=\frac{dy}{dt}\)、 \(k>0\) です。
初期条件(時間 \(t=0\) のときの条件)として位置 \(y(t=0)=0\)、初速度 \(v(t=0)=0\) とします。
ここまでの条件を図でまとめておきます。

ここまでの条件から、速度に比例する抵抗がある場合の落下運動における運動方程式は以下のようになります。
$$
\begin{align}
m\frac{dv}{dt}&=kv^2-mg\tag{1}
\end{align}
$$
(2)微分方程式を解く
ではこの微分方程式を解いていきましょう。
まず式(1)の両辺を \(m\) で割ります。
$$
\begin{align}
\frac{dv}{dt}&=\frac{k}{m}v^2-g\\
\\
&=g\left(\frac{k}{mg}v-1\right)\tag{2}
\end{align}
$$
ここで \(\frac{k}{mg}=K^2\) とおきます。
すると式(2)は次のようになります。
$$
\begin{align}
\frac{dv}{dt}&=g(K^2v^2-1)\tag{3}
\end{align}
$$
これで式がかなりシンプルな形になったと思います。
続いて式(3)を変数分離で解いていきます。左辺に \(v\)、右辺に定数を移項しましょう。すると次式のようになります。
$$
\begin{align}
\frac{dv}{K^2v^2-1}&=gdt\tag{4}
\end{align}
$$
それでは式(4)の両辺を積分してきます。
$$
\begin{align}
\int\frac{dv}{K^2v^2-1}&=g\int dt\tag{5}\
\end{align}
$$
さて、式(5)の左辺の \(\frac{1}{K^2v^2-1}\) を変形して積分しやすい形にしていきます。
具体的には現在分母が \(v\) の2次式ですが、こちらを \(v\) の1次式になるように変形していきます。
式(5)の分母は次式(6)のように因数分解できます。
$$
\begin{align}
\frac{1}{K^2v^2-1}=\frac{1}{(Kv+1)(Kv-1)}\tag{6}
\end{align}
$$
そして式(6)を分母の \(v\) が1次式になるように、定数 \(A,B\) を用いて次式(7)ように式を変形していきます。
$$
\begin{align}
\frac{1}{(Kv+1)(Kv-1)}&=\frac{A}{Kv+1}+\frac{B}{Kv-1}\tag{7}\
\end{align}
$$
続いて式(7)の \(A,B\) を求めていきましょう。
$$
\begin{align}
式(7)\Leftrightarrow\frac{1}{(Kv+1)(Kv-1)}&=\frac{A(Kv-1)+B(Kv+1)}{(Kv+1)(Kv-1)}\\
\\
\Leftrightarrow\frac{1}{(Kv+1)(Kv-1)}&=\frac{(A+B)Kv+(-A+B)}{(Kv+1)(Kv-1)}\tag{8}
\end{align}
$$
式(8)両辺の係数を比較して \(A,B\) を求めていきましょう。
$$
\begin{align}
A+B&=0\\
-A+B&=1
\end{align}
$$
これから \(A,B\) は次のようになります。
$$
\begin{align}
A=-\frac{1}{2},B=\frac{1}{2}
\end{align}
$$
求まった \(A,B\) を式(7)に代入します。
$$
\begin{align}
\frac{1}{(Kv+1)(Kv-1)}&=\frac{A}{Kv+1}+\frac{B}{Kv-1}\\
\\
&=-\frac{1}{2}\frac{1}{Kv+1}+\frac{1}{2}\frac{1}{Kv-1}\\
\\
&=\frac{1}{2}\left(-\frac{1}{Kv+1}+\frac{1}{Kv-1}\right)\tag{9}
\end{align}
$$
これで式(5)を積分する準備ができました。式(5)の左辺に式(9)を代入して、積分計算をしていきます。
$$
\begin{align}
\int\frac{dv}{K^2v^2-1}&=g\int dt\tag{5}\\
\\
\int\frac{1}{2}\left(-\frac{1}{Kv+1}+\frac{1}{Kv-1}\right)dv&=g\int dt\\
\\
\frac{1}{2K}\ln\left|\frac{Kv-1}{Kv+1}\right|&=gt+C’\\
\\
\ln\left|\frac{Kv-1}{Kv+1}\right|&=2gKt+2KC’\\
\\
\ln\left|\frac{Kv-1}{Kv+1}\right|&=e^{2gKt+2KC’}\\
\\
\left|\frac{Kv-1}{Kv+1}\right|&=Ce^{2gKt}\tag{10}
\end{align}
$$
\(C,C’\) は積分定数。ここで式(10)の左辺の絶対値をはずすために、正負について考えていきましょう。
\(Kv≧0\) なので、\(Kv+1≧0\) となります。
一方で \(Kv-1\) については \(v\) の値によって正負が変わります。
\(0<v<\frac{1}{K}\) のとき \(Kv-1<0\)、\(\frac{1}{K}≦v\) のとき \(Kv-1≧0\)となります。
それでは式(10)を場合わけして計算していきましょう。
(1) \(0<v<\frac{1}{K}\) のとき
$$
\begin{align}
-\frac{Kv-1}{Kv+1}&=Ce^{2gKt}\\
\\
-(Kv-1)&=Ce^{2gKt}(Kv+1)\\
\\
-Kv-Ce^{2gKt}Kv&=-1+Ce^{2gKt}\\
\\
-(1+Ce^{2gKt})Kv&=-1+Ce^{2gKt}\\
\\
v&=\frac{1}{K}\cdot\frac{1-Ce^{2gKt}}{1+Ce^{2gKt}}\\
\\
\end{align}
$$
(2) \(\frac{1}{K}≦v\) のとき
$$
\begin{align}
\frac{Kv-1}{Kv+1}&=Ce^{2gKt}\\
\\
Kv-1&=Ce^{2gKt}(Kv+1)\\
\\
Kv-Ce^{2gKt}Kv&=1+Ce^{2gKt}\\
\\
(1-Ce^{2gKt})Kv&=1+Ce^{2gKt}\\
\\
v&=\frac{1}{K}\cdot\frac{1+Ce^{2gKt}}{1-Ce^{2gKt}}\\
\\
\end{align}
$$
(3)初期条件を代入して位置や速度を \(t\) の関数で表す
続いて初期条件を代入して定数 \(C\) を求めていきます。
初期条件は初速度 \(v(t=0)=0\) としていましたので、\(t=0,v=0\) を代入していきます。
(1) \(0<v<\frac{1}{K}\) のとき
$$
\begin{align}
v&=\frac{1}{K}\cdot\frac{1-Ce^{2gKt}}{1+Ce^{2gKt}}\\
\\
0&=\frac{1}{K}\cdot\frac{1-Ce^{2gK\cdot0}}{1+Ce^{2gK\cdot0}} \ \ \ \ (∵t=0,v=0)\\
\\
0&=\frac{1}{K}\cdot\frac{1-C}{1+C}\\
\\
0&=1-C\\
\\
C&=1
\end{align}
$$
よって速度 \(v\) は次のようになります。
$$
\begin{align}
v=\frac{1}{K}\cdot\frac{1-e^{2gKt}}{1+e^{2gKt}}\tag{11}
\end{align}
$$
(2) \(\frac{1}{K}≦v\) のとき
$$
\begin{align}
v&=\frac{1}{K}\cdot\frac{1+Ce^{2gKt}}{1-Ce^{2gKt}}\\
\\
0&=\frac{1}{K}\cdot\frac{1+Ce^{2gK\cdot0}}{1-Ce^{2gK\cdot0}} \ \ \ \ ( ∵ t=0,v=0)\\
\\
0&=\frac{1}{K}\cdot\frac{1+C}{1-C}\\
\\
0&=1+C\\
\\
C&=-1
\end{align}
$$
よって速度 \(v\) は次のようになります。
$$
\begin{align}
v=\frac{1}{K}\cdot\frac{1-e^{2gKt}}{1+e^{2gKt}}\tag{12}
\end{align}
$$
さて式(11)と式(12)を見比べてみると、同じ式になっていることがわかります。
つまり、\(v\) の値に対して \(\frac{1}{K}\) より大きいか小さいかで場合わけをして計算をしてきましたが、実際にはどのような \(v(>0)\) においても、次式で表されます。
$$
\begin{align}
v=\frac{1}{K}\cdot\frac{1-e^{2gKt}}{1+e^{2gKt}}
\end{align}
$$
ここで最初に \(K^2=\frac{k}{mg}\) とおいたので \(K=\sqrt\frac{k}{mg}\) を代入します。すると、
$$
\begin{align}
v=\sqrt\frac{mg}{k}
\cdot\frac{1-e^{2\sqrt\frac{gk}{m}t}}{1+e^{2\sqrt\frac{gk}{m}t}}
\end{align}
$$
ここからは速度 \(v\) の時間変化の特徴を見ていきます。
式を見やすくするために \(v_\infty=\sqrt\frac{mg}{k},c=\sqrt\frac{gk}{m}\) とおきます。
すると \(v\) はつぎのようになります。
$$
\begin{align}
v=v_\infty
\cdot\frac{1-e^{2ct}}{1+e^{2ct}}
\end{align}
$$
式をみると、ネイピア数 \(e\) の指数に時間 \(t\) という変数が含まれています。
こういう場合、\(t\rightarrow\infty\) の極限を取った場合に、ある値に収束するのか?発散するのか?が気になります。
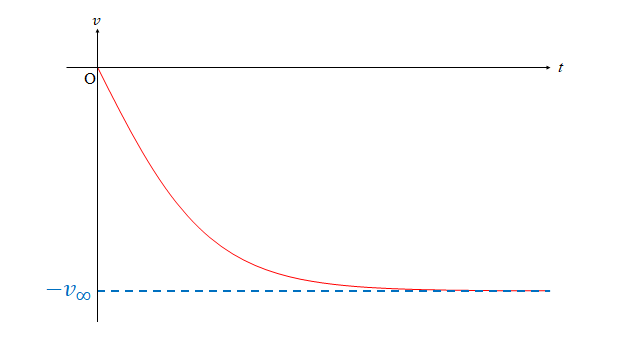
なので、\(t\rightarrow\infty\) の \(v\) について考えていきましょう。
$$
\begin{align}
\lim_{t\rightarrow\infty}v&=\lim_{t\rightarrow\infty}v_\infty
\cdot\frac{1-e^{2ct}}{1+e^{2ct}}\\
\\
&=\lim_{t\rightarrow\infty}v_\infty
\cdot\frac{e^{-2ct}-1}{e^{-2ct}+1}\\
\\
&=v_\infty
\cdot\frac{0-1}{0+1}\\
\\
&=-v_\infty
\end{align}
$$
この結果から、ある一定時間が経過すると、重力と速度の2乗に比例する抵抗がつりあって一定速度になります。このような速度のことを終端速度と呼びます。
速度 \(v\) と時間 \(t\) の関係は次図のようになります。
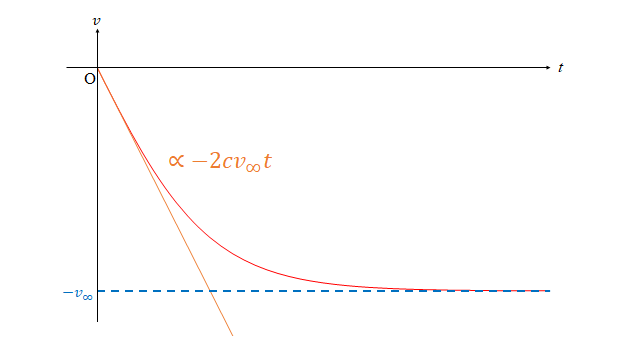
次は \(t=0\) から終端速度に到達するまでの速度について考えます。
まず \(e^x\) の \(x=0\) まわりでのテイラー展開について考えると
$$
\begin{align}
e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+・・・
\end{align}
$$
となります。ここで \(x\ll1\)のとき、\(x\) の2次以上の項は十分に小さいので無視れば、次の1次式に近似できます。
$$
\begin{align}
e^x\simeq1+x
\end{align}
$$
よってテイラー展開による1次近似より、
$$
\begin{align}
e^{2ct}\simeq1+2ct
\end{align}
$$
と近似することができます。
よって速度 \(v\) は
$$
\begin{align}
v&=v_\infty
\cdot\frac{1-e^{2ct}}{1+e^{2ct}}\\
\\
&\simeq v_\infty
\cdot\frac{1-(1+2ct)}{1+(1+2ct)}\\
\\
&= v_\infty
\cdot\frac{-2ct}{2+2ct}
\end{align}
$$
現在 \(2ct\ll1\) で考えているので、
$$
\begin{align}
v\simeq -cv_\infty t
\end{align}
$$
となり、\(t\) が小さいときには \(t\) に比例した \(v\) となることがわかりました。
最後に
今回は速度の2乗に比例する抵抗がある場合の落下運動について考ええました。
これまでとどうように運動方程式を解くときには
(1)成分ごとに運動方程式を立てる
(2)微分方程式を解く
(3)初期条件を代入し、位置や速度を \(t\) の関数で表す
個人的には \(Kv-1\) の正負について場合わけして \(v\) について考えたのに、その後計算していくと \(Kv-1\) の正負にかかわらず \(v\) が1つの式で表されたところが面白かったですね。
また、テイラー展開を利用した近似を用いることで、速度 \(v\) の式を理解しやすい形で式変形できたところが、運動を理解する助けになる感じがしますね。
Baby steps to Giant strides !