今回はベクトル解析で学ぶrot(回転;rotation)について説明していきます。
rotの定義について紹介と、rotのイメージを水流の中に水車の車輪を沈めた状況を設定して具体的にイメージしやすいようにして説明します。
ベクトル解析で学ぶdiv(発散)、grad(勾配)について説明しましたが、それと同様に物理の教科書を理解するためには知っておくべき内容です。
divやgradに比べて定義の式はやや複雑になりますが、何を表しているかというイメージをしっかりもっておけば簡単にその定義を導くこともできます!
rot(回転)の定義とイメージ
rotの定義は次のようになります。
あるベクトル関数\(\boldsymbol V=(V_x,V_y,V_z)\)とすると
$$\mathrm{rot}{ \boldsymbol V} = (\frac{\partial V_{z}}{\partial y} – \frac{\partial V_{y}}{\partial z},\frac{\partial V_{x}}{\partial z} – \frac{\partial V_{z}}{\partial x},\frac{\partial V_{y}}{\partial x} – \frac{\partial V_{x}}{\partial y}) $$
rotはdivやgradに比べると少し定義がややこしいです。
しかもrotの\(z\)成分をみてみると、\(\boldsymbol {V}_y\)を\(x\)で微分していたり、\(\boldsymbol {V}_x\)を\(y\)で微分しています。
この式だけを見てもはっきりいってどこがどのように回転を表しているのかわからなくないですか?
そこでまずは具体的にわかりやすい例をあげてrotのイメージを作っていきましょう!
まずベクトル場においては水流が一番イメージしやすいと思います。
その水流の中に下図のように水車のように真ん中に軸があって回転するようなものを完全に水の中につけたような状態をイメージしてください。
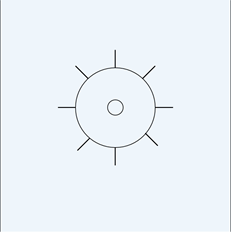
このように水流(ベクトル場)の中にある微小な水車の回転速度について考えるのがrotの意味です。
では、この水車はどのような状況であれば回転しだすでしょうか?
例えば、下図のように右側にホースか何かを入れて、水車の中心より右側のほうで水流が速く、左側のほうで水流が遅いような状況を考えます。
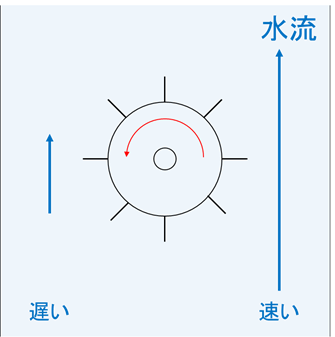
このような状況であれば、水車は反時計回りに回転しだすことが容易に想像できます。
ようするに、水車の右側と左側の水流の速さが違っていれば、水車は回転し始めるということです。
そして、水車の回転するスピードは、水車の右側と左側の水流の速さの差に比例することになります。
rotをイメージから数学的に理解していく
ここまででrotのイメージが掴め始めたと思うので、ここからは少し数学的に説明していきます。
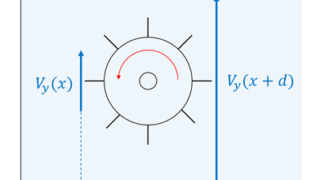
次の図のように、流速を示す関数を\(\boldsymbol {V}_{y}\)、水車の直径を\(d\)とします。
水車の両側の流速について、右側の流速は\(\boldsymbol {V}_{y}(x+d)\)、左側の流速は\(\boldsymbol V_y(x)\)となるので、両側の流速差は\(\boldsymbol {V}_{y}(x+d)- \boldsymbol {V}_{y}(x)\)となります。
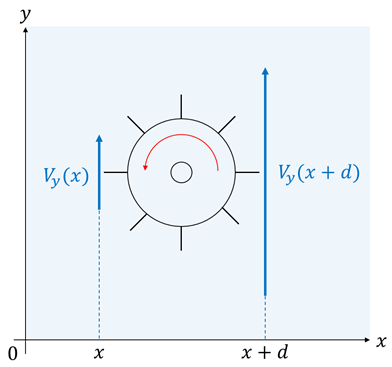
そしてこの左右の流速が水車の回転に対して作用(トルク)しているので、水車の半径で割ることで以下のように回転速度が求まります。
$$\frac{\boldsymbol {V}_{y}(x+d)- \boldsymbol {V}_{y}(x)}{\frac{d}{2}}$$
そしてこの水車の半径を限りなく小さくすると
$$\lim_{\frac{d}{2} \to 0}\frac{\boldsymbol {V}_{y}(x+d)- \boldsymbol {V}_{y}(x)}{\frac{d}{2}}=\frac{\partial \boldsymbol {V}_{y}}{\partial x}$$
となります。
これはrotの\(z\)成分の第1項を表しています。
そして今は流速方向が\(y\)方向である場合について考えたが、今度は流速方向が下図のように\(x\)方向である場合について考えます。
考え方自体は先ほどと全く同様となります。
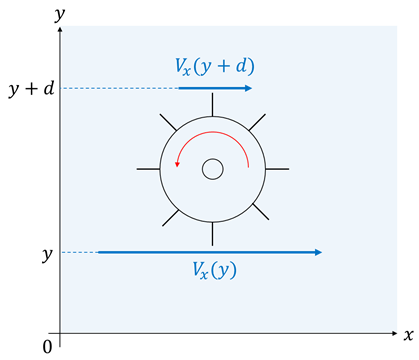
\(x\)方向に流れている水流の流速を示す関数を\(\boldsymbol {V}_{x}\)、水車の直径を\(d\)とします。
水車の上下の流速について、上側の流速は\(\boldsymbol {V}_{x}(y+d)\)、下側の流速は\(\boldsymbol V_x(y)\)となります。
そしてこれらから流速差を考えるのですが、ここで注意をしなければならないのが水車の回転方向です。
先ほど\(y\)方向の水流について考えたときには特に何も語らなかったですが水車の回転は反時計周り方向を正としていました。
そこで、符号を正確にするためにはここでも反時計周りを正として考える必要があります。
よって上下の流速差は\(\boldsymbol{V}_{x}(y)- \boldsymbol {V}_{x}(y+d)\)とする必要があります。
これを先ほどと同様にして水車の半径で割って、半径をできる限り小さくすることによって
$$\lim_{\frac{d}{2} \to 0}\frac{\boldsymbol {V}_{x}(y)- \boldsymbol {V}_{x}(y+d)}{\frac{d}{2}}=-\frac{\partial \boldsymbol {V}_{x}}{\partial y}$$
となります。
これはrotの\(z\)成分の第2項になります。
ここまでで、rotの\(z\)成分である
$$\frac{\partial V_{y}}{\partial x} – \frac{\partial V_{x}}{\partial y} $$
が示されました。
これでだいたいrotの式についてイメージできてきたのではないでしょうか?
つまりrotの\(z\)成分が何を示しているかというと、\(z\)軸を回転軸にもつ\(xy\)平面上の微小領域に対して水流が流れた場合に、左回りにどの程度の速度で回転するかを示していることになります。
\(x\)成分、\(y\)成分についても同様にして計算することで導出することができます。
おすすめの参考書
物理数学の勉強におすすめの参考書を3冊ほど紹介しておきます。
最後に
最後に少しまとめておくと、
rotの定義は次のようになります。
あるベクトル関数\(\boldsymbol V=(V_x,V_y,V_z)\)とすると
$$\mathrm{rot}{ \boldsymbol V} = (\frac{\partial V_{z}}{\partial x} – \frac{\partial V_{y}}{\partial z},\frac{\partial V_{x}}{\partial z} – \frac{\partial V_{z}}{\partial x},\frac{\partial V_{y}}{\partial x} – \frac{\partial V_{x}}{\partial y}) $$
rotはベクトル場の回転を意味しており、より分かりやすく言うとrotの\(z\)成分であれば、\(z\)軸を回転軸にもつ\(xy\)平面上の微小領域に対して水流が流れた場合に、左回りにどの程度の速度で回転するかを示していることになります。
rot(回転)について少しはイメージをもてるようになったでしょうか?
rotなどベクトル解析は電磁気学を学ぶときに使われますが、やはり電磁気学などは目で見えないことについて語られるので物理的なイメージがわきにくいと思います。
そういうときは今回のように水流などイメージしやすい例に置き換えてどのような状況かを理解するようにしましょう。
今回のrotの話がイメージするときの一助になれば幸いです。
Baby steps to Giant strides !







こんにちは。
直観的には一番わかりやすかったのです。
rotの公式のx成分の1項目の分母が∂xではなくて∂yではないかと思いますがどうでしょうか?
わかりやすいとのコメントありがとうございます!
また、間違いの指摘ありがとうございます。
修正いたしました。