【物理】運動方程式(落下運動・放物運動)【力学】

前回までは位置・速度・加速度について学びました。

今回は運動方程式を取り扱います。

具体例として自由落下運動と放物運動を用いて、運動方程式を立てて微分方程式を解き、運動を理解していきます。

Contents

ニュートンの運動法則と運動方程式
例1：自由落下運動
例2：放物運動
おすすめの参考書
最後に

ニュートンの運動法則と運動方程式

ニュートンは物体の観察や経験的事実から3つの基本法則が説明できることを見出しました。この法則を「ニュートンの運動法則」と言います。

ニュートンの運動法則の3つの法則は以下の通りです。

第1法則(慣性の法則)
第2法則(運動法則)
第3法則(作用・反作用の法則)

まずはニュートンの運動法則について説明します。

第1法則(慣性の法則)

物体は外力によって状態を変えられない限り、静止の状態あるいは一直線上の一様な運動をし続ける。

第2法則(運動法則)

質点の運動の変化は、及ぼされる力に比例し、その力が及ぼされる直線方向に起こる。

$\boldsymbol F$：力、$m$：質量、$\boldsymbol r(t)$：質点の位置ベクトル、$\frac{d^2\boldsymbol r}{dt^2}$：加速度として、第2法則を以下の式で表すことができます。
$$
\begin{align}
m\frac{d^2\boldsymbol r}{dt^2}=\boldsymbol F\tag{1}
\end{align}
$$

この式を「運動方程式」といいます。

第3法則(作用・反作用の法則)

質点1が質点2に力を及ぼしているとき、質点2は質点1に大きさが同じで反対向きの力を及ぼしている。

今回はニュートンの運動法則の第2法則にある運動方程式を用います。

力学の目的は何か？それは位置ベクトル $r$ を $t$ の関数で表し、物体が時間ごとにどの位置にいるかという運動の軌跡を知ることです。

これは運動方程式を立てて、微分方程式を解くことによって $\boldsymbol r(t)$ を導くことができます。

そこで以後は具体例を出して、運動方程式を解いていきます。

例1：自由落下運動

具体例として自由落下運動について考えます。

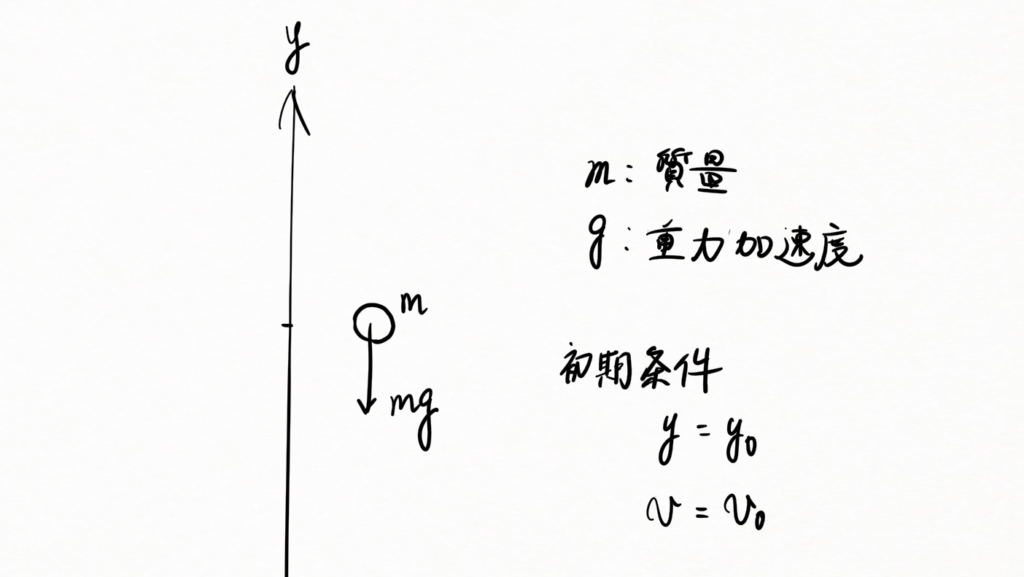
上向きを正として $y$ 軸をとります。別に $x$ 軸としても $z$ 軸としても問題はありません。

地上の物体は全て鉛直下向き(今の設定でいうならば $y$ の負方向)に大きさ $mg$ の力を受けます。

$m$ は質量、$g$ は重力加速度です。初期条件(時間 $t=0$ のときの条件)として位置 $y=y_0 $、初速度 $\frac{dy(0)}{dt}=v_0$ とします。

運動方程式はニュートンの運動法則の第2法則にあったように、以下のようになります。
$$
\begin{align}
m\frac{d^2y}{dt^2}=F
\end{align}
$$

ここで、物体にかかる力は重力のみなので、$F=-mg$ です。符号が負であるの理由は、上向きを正として $y$ 軸をとったので、$y$ 軸方向下向きにはたらく重力は符号が負になります。

よって運動方程式(式(1))に $F=-mg$ を代入すると次のようになります。
$$m\frac{d^2y}{dt^2}=-mg$$
続いて両辺を $m$ で割ります。

$$
\begin{align}
\frac{d^2y}{dt^2}=-g\tag{2}
\end{align}
$$

この式からわかることを考えてみましょう。左辺は加速度を表しており、$g$は重力加速度なので定数です。

つまり、自由落下運動は加速度が時間変化せず、一定であることを示しています。
このような加速度が時間変化しない運動を「等加速度運動」といいます。

続いて式(2)の微分方程式を解いていきましょう。

$$
\begin{align}
\frac{d^2y}{dt^2} & =-g \\
&\Downarrow t積分\\
\frac{dy}{dt} & =-gt+C_1\tag{3}\\
&\Downarrow t積分\\
y & =-\frac{1}{2}gt^2+C_1t+C_2\tag{4}
\end{align}
$$

$C_1,C_2$:積分定数

次は初期条件を用いて積分定数を求めます。初期条件($t=0$)は位置$y=y_0$、初速度 $\frac{dy(0)}{dt}=v_0$です。
この初期条件を式(3)(4)へ代入して計算します。

●式(3)に初期条件代入
$$
\begin{align}
\frac{dy}{dt}&=-gt+C_1\\
&\Downarrow t=0,\frac{dy(0)}{dt}=v_0代入\\
v_0&=-g\cdot0+C_1\\
&\Downarrow\\
C_1&=v_0
\end{align}
$$

●式(4)に初期条件代入
$$
\begin{align}
y&=-\frac{1}{2}gt^2+C_1t+C_2\\
&\Downarrow t=0,y=y_0代入\\
y_0&=-\frac{1}{2}g\cdot0^2+C_1\cdot 0+C_2\\
&\Downarrow\\
y_0&=0+0+C_2\\
&\Downarrow\\
C_2&=y_0
\end{align}
$$

これで積分定数$C_1,C_2$が求まりました。
求まった積分定数を式(4)に代入することで $y(t)$ を求めるができます。

●式(4)に積分定数$C_1,C_2$代入
$$
\begin{align}
y & =-\frac{1}{2}gt^2+C_1t+C_2\\
&\Downarrow C_1=v_0,C_2=y_0代入\\
y & =-\frac{1}{2}gt^2+v_0t+y_0\\
\end{align}
$$

以上より、自由落下運動のときの位置 $y$ を $t$ の関数で表すことができました。

$$
\begin{align}
y(t) & =-\frac{1}{2}gt^2+v_0t+y_0
\end{align}
$$

例2：放物運動

次に具体例として放物運動について考えます。

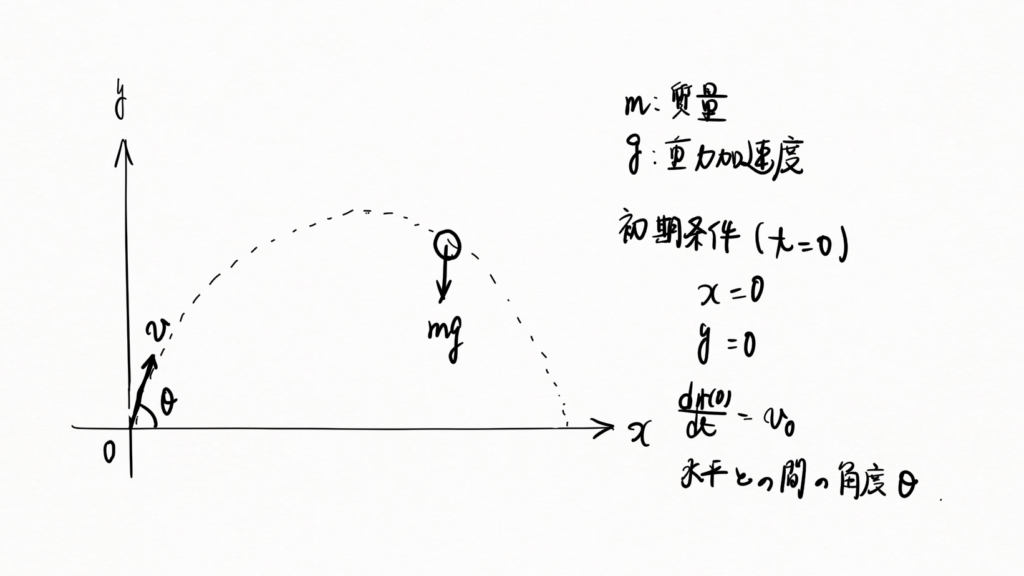
水平方向右向きを正として $x$ 軸をとり、鉛直上向きを正として $y$ 軸をとります。

地上の物体は全て鉛直下向き ($y$ の負方向)に大きさ $mg$ の重力を受けます。 $m$ は質量、 $g$ は重力加速度です。初期条件(時間 $t=0$ のときの条件)として位置$x=0,y=0$、初速度 $v_{0}$ で水平との間の角度 $\theta$ とします。

ここで運動方程式を書いていくのですが、成分ごと($x$成分、$y$成分)に運動方程式を立てて計算していきます。
$$
\begin{align}
x成分：m\frac{d^2x}{dt^2}&=0　\\
y成分：m\frac{d^2y}{dt^2}&=-mg
\end{align}
$$
続いてこれらの運動方程式を成分ごとに解いていきます。

●$x$成分
$$
\begin{align}
m\frac{d^2x}{dt^2}&=0　\\
&\Downarrow t積分\\
\frac{dx}{dt}&=C_1　\\
&\Downarrow t積分\\
x&=C_1t+C_2　\\
\end{align}
$$
ただし$C_1,C_2$は積分定数です。

初期条件より $t=0$ のとき $\frac{dx}{dt}=v_0\cos\theta,x=0$であるから
$$
\begin{align}
\frac{dx}{dt}&=C_1　\\
&\Downarrow \frac{dx}{dt}=v_0\cos\theta代入\\
C_1&=v_0\cos\theta　\\
\end{align}
$$

$$
\begin{align}
x&=C_1t+C_2　\\
&\Downarrow t=0,x=0代入\\
C_2&=0　\\
\end{align}
$$
以上より $x$は$t$の関数として以下の式のようになります。
$$
\begin{align}
x&=C_1t+C_2\\
&=v_0\cos\theta\cdot t+0\\
&=v_0t\cos\theta
\end{align}
$$

●$y$成分
$$
\begin{align}
m\frac{d^2y}{dt^2}&=-mg　\\
&\Downarrow t積分\\
\frac{dy}{dy}&=-gt+C_3　\\
&\Downarrow t積分\\
y&=-\frac{1}{2}gt^2+C_3t+C_4　\\
\end{align}
$$
ただし$C_3,C_4$は積分定数です。

初期条件より $t=0$ のとき $\frac{dx}{dt}=v_0\sin\theta,x=0$であるから
$$
\begin{align}
\frac{dy}{dt}&=-gt+C_3　\\
&\Downarrow t=0,\frac{dy}{dt}=v_0\sin\theta代入\\
C_3&=v_0\sin\theta　\\
\end{align}
$$

$$
\begin{align}
y&=-\frac{1}{2}gt^2+C_3t+C_4　\\
&\Downarrow t=0,y=0代入\\
C_4&=0　\\
\end{align}
$$
以上より $y$ は $t$ の関数として以下の式のようになります。
$$
\begin{align}
y&=-\frac{1}{2}gt^2+C_3t+C_4\\
&=-\frac{1}{2}gt^2+v_0\cos\theta\cdot t+0\\
&=-\frac{1}{2}gt^2+v_0t\cos\theta
\end{align}
$$

ここまで運動方程式を解くことで、放物運動するときの位置 $x,y$ を $t$ の関数で表すことができたのでまとめておきます。

$$ \begin{align}
x &= v_0t\cos\theta\\
y &= -\frac{1}{2}gt^2+v_0t\cos\theta
\end{align} $$