今回は力学の基礎である1次元空間の位置・速度・加速度について説明します。
力学では物体の間に作用する力とそれら物体の運動との関係を調べます。
運動は時間とともに位置・速度・加速度がどのように変化するかによって記述されます。
だから力学を勉強する上で位置・速度・加速度はもっとも基本的な概念になります。
1次元空間における位置・速度・加速度
1.1 位置
1次元空間の点の移動について考えていきます。
1次元空間の点の移動とは上下方向や左右方向など直線上の点の移動のことです。
一次元空間における運動の具体例をあげると、人がまっすぐ歩く・ボールを真下に落とすような運動のことです。
下図のように一次元空間にある点Pの運動について考えます。
点Pの位置を座標で表し、座標軸を\(x\)軸とします。
時刻tにおける点Pの位置を \( x(t) \) と表します。
例えば時刻 \( t=t_0 \) のときの点Pの位置は \( x(t_0) \) と表し、時刻 \( t=t_0+ \Delta t \) のときの点Pの位置は \( x(t_0+ \Delta t) \) と表します。
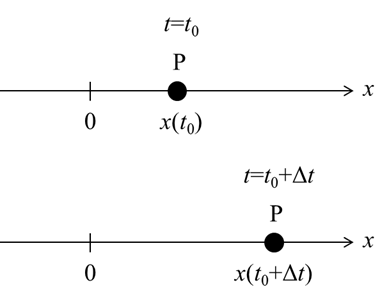
このとき時刻 \( t_0 \) から \( t_0+ \Delta t \) における点Pの位置の変化はどのようになるでしょうか?
位置の変化=変化後の位置-変化前の位置
で表せます。
時刻 \( t_0 \) のときの点Pの位置は \( x(t_0) \) 、時刻 \( t_0+ \Delta t \) のときの点Pの位置は \( x(t_0+ \Delta t) \) ですので、
時刻 \( t_0 \) から \( t_0+ \Delta t \) における点Pの位置の変化 \( =x(t_0+ \Delta t)-x(t_0) \)
と表すことができます。
1.2 速度
速度とは単位時間あたりの位置の変化のことであり、向きについても考えるベクトル量です。
よく似た意味で速さがありますが、速さは速度とは異なり向きは考えません。
速度は\(v\)(velocity)で表されることが一般的です。
速度の定義は次のようになります。
$$\begin{align}速度 &=\frac{位置の変化}{かかった時間}\\ &=\frac{変化後の位置 – 変化前の位置}{変化後の時間 – 変化前の時間}\end{align}$$
ただしこの速度はある程度の時間間隔の間の速度、すなわち平均速度を表しています。
このままではある時刻における速度=瞬間の速度はわかりません。
ある時刻における位置を表すために\(x-t\)グラフを書いてみましょう。
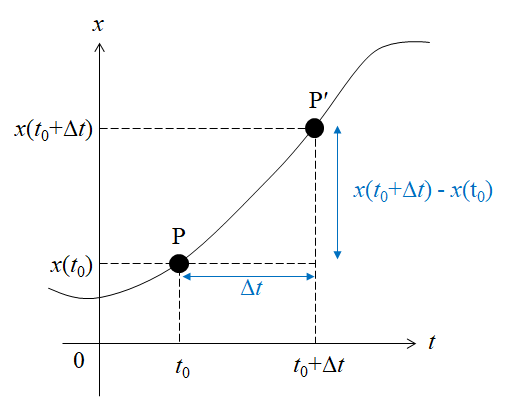
時刻 \( t_0 \) のときに位置\(x(t_0)\)にいる点をP
時刻\(t_0+ \Delta t\)のときに位置\(x(t_0+ \Delta t)\)にいる点をP’とします。
このとき点Pから点P’に移動する間の速度は以下のように表せます。
$$速度=\frac{x(t_0+ \Delta t)-x(t_0)}{ \Delta t}$$
次に点P’をさらに点Pに近づけます。
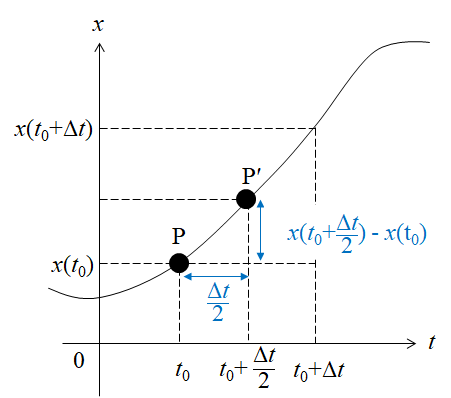
このとき点Pから点P’に移動する間の速度は以下のように表せます。
$$速度=\frac{x(t_0+\frac{\Delta t}{2}) – x(t_0)}{\Delta t}$$
このようにして点P’を限りなく点Pに近づけていきます。
最初点Pと点P’の変化後の時間-変化前の時間\(= \Delta t\)でしたが、 \(\Delta t\rightarrow 0\)に近づけていくわけです。
これによって点Pにおける瞬間の速度を求めることができます。
点Pにおける速度を\(v\)とすると
$$v =\lim_{\Delta t \rightarrow 0} \frac{x(t_0 +\Delta t)-x(t_0)}{\Delta t}$$
これはいわゆる微分の定義です。
つまり速度は以下のようになります。
$$\begin{align} v &=\lim_{\Delta t \rightarrow 0} \frac{x(t_0 +\Delta t)-x(t_0)}{\Delta t} \\&=\frac{d x}{d t}\end{align}$$
ある点における速度をしりたければ位置を時間で微分することで求めることができます。
また物理学においては時間に関する微分をドット「・」を用いて以下のように表現する場合があります。
$$v =\dot x=\frac{dx}{dt}$$
力学においては基本的に速度=瞬間速度になります。覚えておきましょう。
1.3 加速度
加速度とは単位時間あたりの速度の変化のことであり、向きについても考えるベクトル量です。
加速度は\(a\)(acceleration)で表されることが一般的です。
加速度の定義を式で表すと次のようになります。
$$\begin{align}加速度&=\frac{速度の変化}{かかった時間}\\ &=\frac{変化後の速度-変化前の速度}{変化後の時間-変化前の時間}\end{align}$$
この加速度の式の先ほど示した速度の式を見比べてみましょう。
$$\begin{align}速度 &=\frac{位置の変化}{かかった時間}\\ &=\frac{変化後の位置 – 変化前の位置}{変化後の時間 – 変化前の時間}\end{align}$$
比較すると明確ですが、よく似た定義になっています。
加速度も先ほどの速度と同様にある点における加速度=瞬間加速度を知りたいのですが、これは先ほどの速度について考えたときと同様の考え方が使えます。
変化後の点を変化前の点にできる限り近づけていく考え方です。
ある時刻における速度を表すために\(v-t\)グラフを書きます。
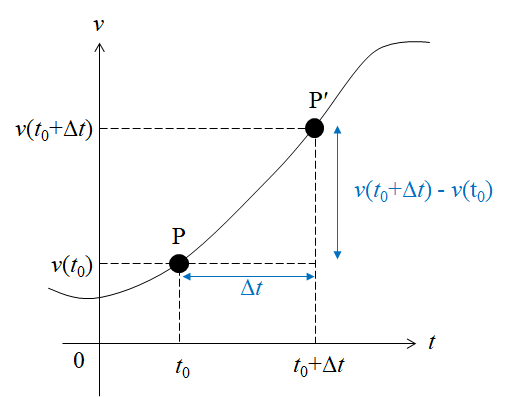
時刻\(t_0\)のときに速度\(v(t_0)\)である点をP
時刻\(t_0+_\Delta t\)のときに速度\(v(t_0+\Delta t)\)である点をP’とします。
このとき点Pから点P’に移動する間の加速度は以下のように表せます。
$$a=\frac{v(t_0+ \Delta t)-v(t_0)}{ \Delta t}$$
これを\(\Delta t \rightarrow 0\)に近づけていきます。
これによって点Pにおける瞬間の加速度を求めることができます。
つまり加速度は以下のようになります。
$$\begin{align} a &=\lim_{\Delta t \rightarrow 0} \frac{v(t_0 +\Delta t)-v(t_0)}{\Delta t} \\&=\frac{d v}{d t}\end{align}$$
ある点における加速度をしりたければ速度を時間で微分することで求めることができます。
また速度のときに\( v =\dot x\)と表したのと同様に、加速度においても時間に関する微分をドット「・」を用いて以下のように表現する場合があります。
$$a =\dot v=\frac{dv}{dt}$$
さらに加速度\(a\)は速度 \(v\) を用いて表しており、 速度 \(v\) は 位置 \(x\) を用いて表されています。
なので当然、加速度\(a\) は 位置 \(x\) を用いて表すこともできます。
$$\begin{align}a &= \frac{dv}{dt}\\ &= \frac{d}{dt}(\frac{dx}{dt})\\ &= \frac{d^2 x}{dt^2}\end{align}$$
また、 ドット「・」を用いて以下のように表現する場合があります。
$$a = \dot v=\frac{dv}{dt} =\ddot x = \frac{d^2 x}{dt^2} $$
力学においては基本的に加速度=瞬間加速度になります。覚えておきましょう。
まとめ
一次元空間における位置・速度・加速度についてまとめておきましょう。
$$\begin{align} v &=\lim_{\Delta t \rightarrow 0} \frac{x(t_0 +\Delta t)-x(t_0)}{\Delta t} =\frac{d x}{d t}\\ a &=\lim_{\Delta t \rightarrow 0} \frac{v(t_0 +\Delta t)-v(t_0)}{\Delta t} =\frac{d v}{d t}\end{align}$$
$$\begin{align}v &=\dot x=\frac{dx}{dt} \\a &= \dot v=\frac{dv}{dt} =\ddot x = \frac{d^2 x}{dt^2}\end{align} $$
位置と時間の関係さえわかれば、速度・加速度を求めることができそうですね。
Baby steps to Giant strides !