前回はばねにつながれたおもりの運動による単振動について考えました。
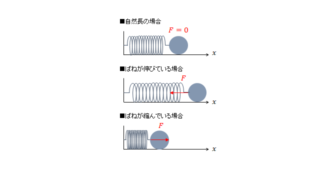
しかし実際にはばねにおもりをつけて振動させると、床との摩擦や空気抵抗など何らかの抵抗を受けて、振動が少しずつ弱まり、最後には振動が止まってしまうのが普通です。
そこで今回はばね運動に加えて、速度に比例する抵抗が加わったときの運動。すなわち「減衰振動」について考えていきます。
減衰振動
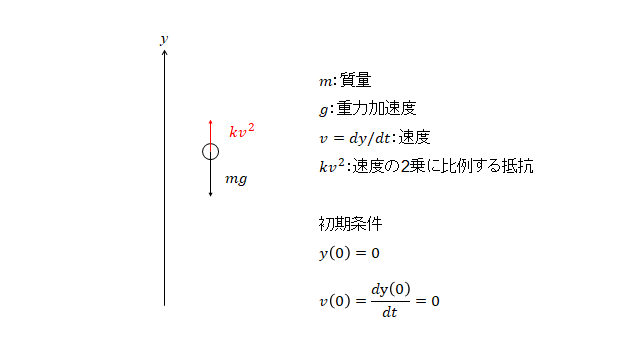
単振動に加えて速度に比例する抵抗が加わったときの運動方程式は次のようになります。
$$m\frac{d^2x}{dt^2}=-kx-B\frac{dx}{dt}$$
右辺の第1項 $-kx$ が復元力、第2項 $-B\frac{dx}{dt}$ が抵抗力を表します。両辺を $m$ で割ると、
$$\frac{d^2x}{dt^2}=-\frac{k}{m}x-\frac{B}{m}\frac{dx}{dt}$$
式を簡単にするために
$$\frac{k}{m}=\omega_0^2, \frac{B}{m}=2\gamma$$
とすると、
$$\frac{d^2x}{dt^2}=-\omega_0^2x-2\gamma\frac{dx}{dt}\\$$
となります。さらに移項をすることで次のような式になります。
$$\frac{d^2x}{dt^2}+2\gamma\frac{dx}{dt}+\omega_0^2x=0$$
次はこの2階線形微分方程式を解いていきます。ここでは微分方程式の解き方のみを書いていきます。
$x=e^{\lambda t}$ とおいて代入すると、
$$\begin{aligned}\lambda^2e^{\lambda t}+2\gamma\lambda e^{\lambda t}+\omega_0^2e^{\lambda t}=0\\ \ \\(\lambda^2+2\gamma\lambda+\omega_0^2)e^{\lambda t}=0\end{aligned}$$
$e^{\lambda t}>0$ なので
$$\lambda^2+2\gamma\lambda+\omega_0^2=0$$
となり、この $\lambda$ についての2次方程式を解くと、
$$\lambda_\pm=\frac{-2\gamma\pm\sqrt{4\gamma^2-4\omega_0^2}}{2}\\
\ \\
=-\gamma\pm\sqrt{\gamma^2-\omega_0^2}$$
となります。ここで、$\gamma$, $\omega_0$ の大小関係によって運動の様子が変わります。そこで場合わけをして考えていきます。
(1) $\omega_0>\gamma$ (減衰振動)のとき
$\omega_0>\gamma$ のときがどのような状況なのかというと、$\omega_0$ は復元力の因子、$\gamma$ は抵抗力の因子となります。
つまり、$\omega_0>\gamma$ は抵抗力に対して復元力がおもりに強く作用していることを表しています。 $\omega’^2=\omega_0^2-\gamma^2$ とおくと、
$$\begin{aligned}\lambda_\pm&=-\gamma\pm\sqrt{\gamma^2-\omega_0^2}\\\ \\&=-\gamma\pm\sqrt{-(\omega_0^2+\gamma^2)}\\\ \\&=-\gamma\pm i\sqrt{\omega’^2}\\\ \\&=-\gamma\pm i\omega’\end{aligned}$$
つまり一般解は任意の定数 $A,B$ を用いて、
$$\begin{aligned}x&=Ae^{\lambda_+t}+Be^{\lambda_-t}\\\ \\&=Ae^{(-\gamma+ i\omega’)t}+Be^{(-\gamma- i\omega’)t}\\\ \\&=e^{-\gamma t}(Ae^{i\omega’t}+Be^{- i\omega’t})\end{aligned}$$
さてこれで $x$ の一般解が求まったわけですが、これでは運動の様子がイマイチ上手く読み取れません。そこで、オイラーの公式を用いて、指数関数を三角関数の形に変えます。
■オイラーの公式
$$e^{\pm i\theta} = \cos\theta \pm i\sin\theta$$
$$\begin{aligned}x&=e^{-\gamma t}(Ae^{i\omega’t}+Be^{- i\omega’t})\\\ \\&=e^{-\gamma t}\{A(\cos\omega’t+i\sin\omega’t)+B(\cos\omega’t-i\sin\omega’t)\}\\\ \\&=e^{-\gamma t}\{(A+B)\cos\omega’t+i(A-B)\sin\omega’t\}\end{aligned}$$
$A+B=C’, i(A-B)=C”$ とおき、式を整理します。$C’, C”$ は任意の定数です。そして三角関数の合成により式変形を行います。
■三角関数の合成
$$\begin{aligned}a\sin\theta+b\cos\theta=\sqrt{a^2+b^2}\cos(\theta+\phi), \ \ \tan\phi=-\frac{b}{a}\end{aligned}$$
$$\begin{aligned}x&=e^{-\gamma t}(C’\cos\omega’t+C”\sin\omega’t)\\\\&=Ce^{-\gamma t}\cos(\omega’t+\phi)\\\end{aligned}$$
ただし、$C=\sqrt{C’^2+C”^2}$、$\tan\phi=-\frac{C”}{C’}$ となります。運動の様子を以下に図示します。

このように振動しつつ振幅が減衰していきます。このような運動を減衰振動といいます。
(2) $\omega_0<\gamma$ (過減衰)のとき
$\omega_0<\gamma$ のときがどのような状況なのかというと、$\omega_0$ は復元力の因子、$\gamma$ は抵抗力の因子なので、$\omega_0<\gamma$ は抵抗力が復元力よりもおもりに強く作用していることを表しています。
$$\begin{aligned}\lambda_\pm=-\gamma\pm\sqrt{\gamma^2-\omega_0^2}\end{aligned}$$
いま $\omega_0<\gamma$ なので $\omega_0^2<\gamma^2$ となります。だから、$0<\sqrt{\gamma^2-\omega_0^2}<\gamma$ となるので、$\lambda_\pm$ の2根は共に負の数になります。そして一般解は
$$\begin{aligned}x&=C_1e^{\lambda_+t}+C_2e^{\lambda_-t}\end{aligned}$$
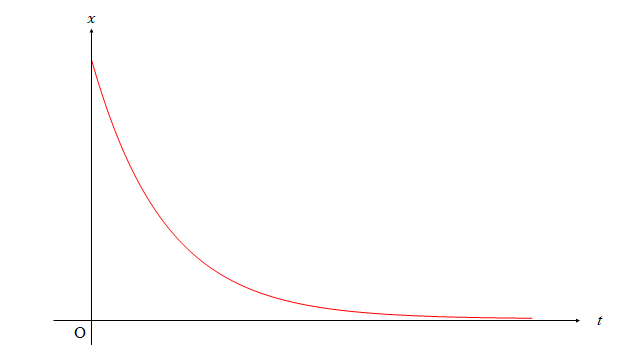
常に$\lambda_\pm$ の2根は負の数になるので、各項は単調減少します。つまり、つまりこの条件のときは振動はしません。 このような運動を過減衰といいます。
(3) $\omega_0=\gamma$ (臨界減衰)のとき
$\omega_0=\gamma$ のとき $\lambda_+=\lambda_-=\gamma$ と置きます。このように $\lambda_\pm$ が重解となるときの一般解は定数 $C,D$ を用いて
$$\begin{aligned}x=(C+Dt)e^{\gamma t}\end{aligned}$$
となります。この運動は下図のようになります。
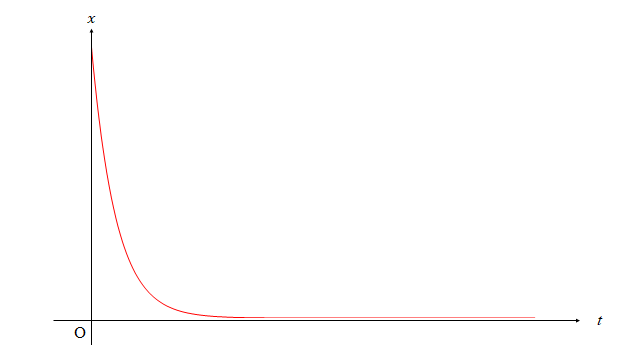
このように $\omega_0=\gamma$ の場合、振動せずに減衰します。この場合、変位 $x$ は最も速く $0$ に減衰し、このような運動を臨界減衰といいます。
最後に
今回は減衰振動について考えていきました。考えた運動方程式は
$$m\frac{d^2x}{dt^2}=-kx-B\frac{dx}{dt}$$
です。$\frac{k}{m}=\omega_0^2, \frac{B}{m}=2\gamma$ として運動方程式を解くと、
(1) $\omega_0>\gamma$ (減衰振動)のとき
$$\begin{aligned}x&=Ce^{-\gamma t}\cos(\omega’t+\phi)\\\end{aligned}$$
(2) $\omega_0<\gamma$ (過減衰)のとき
$$\begin{aligned}x=C_1e^{\lambda_+t}+C_2e^{\lambda_-t}\end{aligned}$$
(3) $\omega_0=\gamma$ (臨界減衰)のとき
$$\begin{aligned}x=(C+Dt)e^{\gamma t}\end{aligned}$$
となります。減衰振動は $\omega_0$ と $\gamma$ の関係によって運動の様子が変化していくのがおもしろいですね!
Baby steps to Giant strides !