複数の振動子系が相互作用を及ぼすとき、その運動を連成振動と呼びます。連成振動は例として格子振動と呼ばれる固体中の原子の振動に近似でき、固体物理の分野でモデルとして使われます。ここでは3つの質点がばねによってつながれた場合の連成振動について考えていきます。
3質点系の連成振動

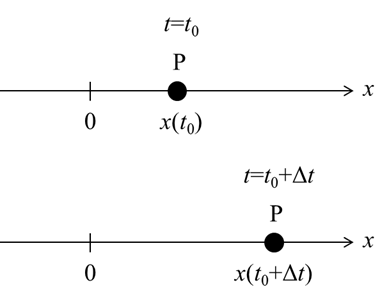
上図のように壁とばねでつながれている3質点系を考えます。
3つの質点の質量は全て$m$、ばね定数は全て$k$とします。
3質点の平衡位置からの変位を$x_1,x_2,x_3$と表すと、各質点に対して、
\begin{eqnarray}
m\frac{d^2x_1}{dt^2}&=&-kx_1-k(x_1-x_2)\\
m\frac{d^2x_2}{dt^2}&=&-k(x_2-x_1)-k(x_2-x_3)\\
m\frac{d^2x_3}{dt^2}&=&-k(x_3-x_2)-kx_3
\end{eqnarray}
のような運動方程式が成り立ちます。これらの式を整理すると、
\begin{eqnarray}
m\frac{d^2x_1}{dt^2}&=&-k(2x_1-x_2)\tag{1}\\
m\frac{d^2x_2}{dt^2}&=&-k(2x_2-x_1-x_3)\tag{2}\\
m\frac{d^2x_3}{dt^2}&=&-k(2x_3-x_2)\tag{3}
\end{eqnarray}
となります。この運動方程式を解いていきます。これらの解を
\begin{eqnarray}
x_1=A_1e^{i\omega t},x_2=A_2e^{i\omega t},x_3=A_3e^{i\omega t}\tag{4}
\end{eqnarray}
と仮定すると、式(4)を式(1)(2)(3)に代入して、
\begin{eqnarray}
m(i\omega)^2A_1e^{i\omega t}&=&-k(2A_1-A_2)e^{i\omega t}\\
m(i\omega)^2A_2e^{i\omega t}&=&-k(2A_2-A_1-A_3)e^{i\omega t}\\
m(i\omega)^2A_3e^{i\omega t}&=&-k(2A_3-A_2)e^{i\omega t}
\end{eqnarray}
となります。これらの式を整理すると、
\begin{eqnarray}
\left\{
\begin{array}{l}
-m\omega^2A_1=-k(2A_1-A_2)\\
-m\omega^2A_2=-k(2A_2-A_1-A_3)\\
-m\omega^2A_3=-k(2A_3-A_2)
\end{array}
\right.\\
\Leftrightarrow
\left\{
\begin{array}{l}
(2k-m\omega^2)A_1-kA_2=0\\
-kA_1+(2k-m\omega^2)A_2-kA_3=0\\
-kA_2+(2k-m\omega^2)A_3=0
\end{array}
\right.
\end{eqnarray}
となります。$A_1=A_2=A_3=0$以外の解を持つ条件は、$A_1、A_2、A_3$の係数行列式が$0$という条件で与えられるので、
\begin{eqnarray}
\left|
\begin{array}{ccc}
2k-m\omega^2 & -k & 0 \\
-k & 2k-m\omega^2 & -k \\
0 & -k & 2k-m\omega^2
\end{array}
\right|=0
\end{eqnarray}
となります。この行列式を計算すると、
\begin{eqnarray}
(2k-m\omega^2)\left|
\begin{array}{ccc}
2k-m\omega^2 & -k \\
-k & 2k-m\omega^2
\end{array}
\right|
-(-k)\left|
\begin{array}{ccc}
-k & 0 \\
-k & 2k-m\omega^2
\end{array}
\right|&=&0\\
(2k-m\omega^2)\{(2k-m\omega^2)^2-(-k)^2\}+k\{-k(2k-m\omega^2)\}&=&0\\(2k-m\omega^2)\{(2k-m\omega^2)^2-(-k)^2-k^2\}&=&0\\
(2k-m\omega^2)(2k^2-4km\omega^2+m^2\omega^2)&=&0\tag{5}
\end{eqnarray}
となり、式(5)を満たす$\omega$の値として、
\begin{eqnarray}
\omega_1&=&\sqrt{2-\sqrt{2}}\omega_0\\
\omega_2&=&\sqrt{2}\omega_0\\
\omega_3&=&\sqrt{2+\sqrt{2}}\omega_0
\end{eqnarray}
が得られます。ただし、$\omega_0\equiv\sqrt{k/m}$とします。
ここで$\omega_1,\omega_2,\omega_3$のそれぞれ場合における$x_1,x_2,x_3$を求めていきます。
(1)$\omega=\omega_1$のとき
式(12)より、$A_1:A_2:A_3=1:\sqrt{2}:1$となります。
一般に$x_1=A_1e^{i\omega t},x_2=A_2e^{i\omega t},x_3=A_3e^{i\omega t}$が解ならば、$x_1=A_1^*e^{-i\omega t},x_2=A_2^*e^{-i\omega t},x_3=A_3^*e^{-i\omega t}$も解になっていることを用いると、$A_1=a_1e^{i\theta_1}$($a_1,\theta_1$:実数)とおいて実数解は
\begin{eqnarray}
x_1&=&a_1\cos(\omega_1t+\theta_1)\\
x_2&=&\sqrt{2}a_1\cos(\omega_1t+\theta_1)\\
x_3&=&a_1\cos(\omega_1t+\theta_1)
\end{eqnarray}
が得られます。
(2)$\omega=\omega_2$のとき
式(12)より、$A_1:A_3=1:-1,A_2=0$となります。
よってこの場合、$A_1=a_2e^{i\theta_2}$($a_2,\theta_2$:実数)とおいて実数解は
\begin{eqnarray}
x_1&=&a_2\cos(\omega_2t+\theta_2)\\
x_2&=&0\\ x_3&=&-a_2\cos(\omega_2t+\theta_2)
\end{eqnarray}
が得られます。
(3)$\omega=\omega_3$のとき
式(12)より、$A_1:A_2:A_3=1:-\sqrt{2}:1$となります。
よってこの場合、$A_1=a_3e^{i\theta_3}$($a_3,\theta_3$:実数)とおいて実数解は
\begin{eqnarray}
x_1&=&a_3\cos(\omega_3t+\theta_3)\\
x_2&=&-\sqrt{2}a_3\cos(\omega_3t+\theta_3)\\
x_3&=&a_3\cos(\omega_3t+\theta_3)
\end{eqnarray}
が得られます。
以上より一般解は、3つの独立な解の重ね合わせから、
\begin{eqnarray}
x_1&=&a_1\cos(\omega_1t+\theta_1)+a_2\cos(\omega_2t+\theta_2)+a_3\cos(\omega_3t+\theta_3)\\
x_2&=&\sqrt{2}a_1\cos(\omega_1t+\theta_1)-\sqrt{2}a_3\cos(\omega_3t+\theta_3)\\ x_3&=&a_1\cos(\omega_1t+\theta_1)-a_2\cos(\omega_2t+\theta_2)+a_3\cos(\omega_3t+\theta_3)
\end{eqnarray}
となります。この式の未知数$a_1,a_2,a_3,\theta_1,\theta_2,\theta_3$は初期条件$t=0$における$x_1,x_2,x_3,dx_1/dt,dx_2/dt,dx_3/dt$によって一意に定まります。以上より各質点の運動は3つの単振動の重ね合わせで表せることがわかりました。このような複数の単振動の合成で変位が表されるときのそれぞれの振動のことを基準振動と呼びます。基準振動のパターンについて考えます。
(a)$a_1\neq0$かつ$a_2=a_3=0$のとき
3つの質点はすべて$\cos(\omega_1t+\theta_1)$に比例する単振動を行い、その振幅の比は$a_1:\sqrt{2}a_1:a_1=1:\sqrt{2}:1$となります。
(b)$a_2\neq0$かつ$a_1=a_3=0$のとき
両端の質点は$\cos(\omega_2t+\theta_2)$に比例する単振動を行い、その振幅の比は$a_2:-a_2=1:-1$であり、中央の質点は振幅$0$で固定されたような状態となります。
(c)$a_3\neq0$かつ$a_1=a_2=0$のとき
3つの質点はすべて$\cos(\omega_3t+\theta_3)$に比例する単振動を行い、その振幅の比は$a_3:-\sqrt{2}a_3:a_3=1:-\sqrt{2}:1$となります。
これらの基準振動を図示すると下図になります。最初の図のように本来は横方向に質点が移動するのですが、振動の様子を見やすくするために、右方向への変位を上、左方向の変位を下として書き直しています。