今回はベクトル解析で学ぶdiv(発散;divergence)について説明していきます。
大学等で物理数学を学ぶときはdivの定義を丸暗記してテストを乗り切ったものの、物理的意味については全く理解していなかったりしませんか?
大学のテストを乗り切るだけならそれで十分な場合が多いですが、物理的意味について理解していなければ、より専門的な物理について勉強するときに意味が理解できずに躓いてしまい、苦労することになります。
物理を学ぶためになぜ数学を学ばなければならないんだ!?という人もいるかもしれませんが、物理を学ぶための共通言語・ツールとして数学を利用するので、勉強せざるを得ません。
この物理数学を理解しておくかどうかで、後々の物理の理解度が大きく変わってきます。
定義を暗記するのではなく、現象として理解するように努めましょう。
div(発散)の定義
divの定義は次のようになります。
あるベクトル場\(\boldsymbol V=(V_x,V_y,V_z)\)とすると
$$\mathrm{div}{ \boldsymbol V} = \frac{\partial V_{x}}{\partial x} + \frac{\partial V_{y}}{\partial y} + \frac{\partial V_{z}}{\partial z} $$
定義を見るとdivはあるベクトル場Vの各成分Vx, Vy, Vzを偏微分したものの和になっています。
定義自体はシンプルで覚えやすいと思います。
ただ、これではいまいち意味が分からない人も多いと思います。
そこで、これがどのような意味を持っているかについて考えていきましょう。
div(発散)の意味の導出
具体例(水の流れをイメージ)
まず、divは「発散」と出てくることが多いと思いますが、ベクトル解析においてはどちらかというと「湧き出し」というイメージを持っておいたほうが理解しやすいと思います。
divの具体例として水の流れをイメージするのが一番わかりやすいです。
例えば川のような水の流れの中に立方体を入れたとします。
すると下の図のようにいろいろな方向から水が立方体の中に流入し、立方体の外に水が流出していくのがイメージできると思います。
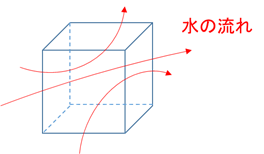
そしてこの立方体に対して正味の流出量(どれだけ水が湧き出したか)を考えます。
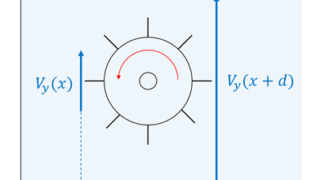
わかりやすくするために、下図のように全体の水の流れをx,y,z方向にそれぞれ分解します。
添えられている数字はそれぞれの方向から流入(および流出)している水の量と考えてください。

すると
- (立方体へ流入する水の量)=3+2+1=6
- (立方体から流出する水の量)=3+1+4=8
となります。
よって(正味の流出量)=(立方体から流出する水の量)―(立方体へ流入する水の量)となるので、
(正味の流出量)=8-6=2
となることがわかりました。
ここでは理解しやすさのために、ある適当な立方体において具体的な数字を用いて正味の流出量を計算しましたが、この立方体を微小体積で正味の流出量を考えたものがdivとなります。
divの一般的意味について
続いてdivについてより厳密に考えていきます。
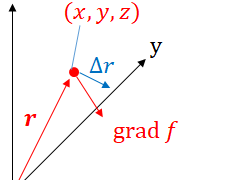
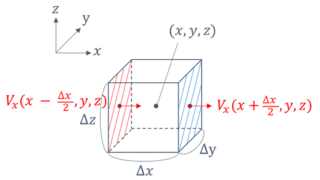
下図のように3次元空間において、ある点(x,y,z)を中心として縦横高さがΔx,Δy,Δzとなる微小直方体があるとします。
この微小直方体に対して流入する水の量と流出する水の量について考えます。
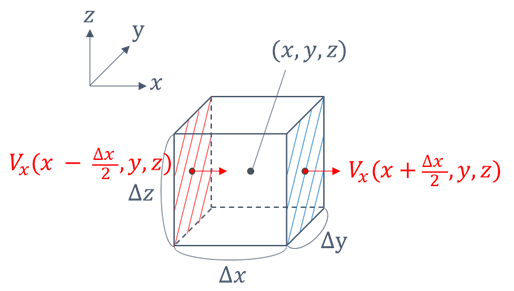
上図の赤い斜線の面からの流入量と青い斜線の面からの流出量について考えます。
赤い斜線面からの流入量は\( V_x(x-\frac{\Delta x}{2},y,z) \Delta y \Delta z\)となり、
青い斜線面からの流出量は\( V_x(x+\frac{\Delta x}{2},y,z) \Delta y \Delta z\)
となります。
$$\begin{align} (流出量)-(流入量) &= V_x(x+\frac{\Delta x}{2},y,z) \Delta y \Delta z – V_x(x-\frac{ \Delta x}{2},y,z) \Delta y \Delta z\\ &= \{V_x(x+\frac{\Delta x}{2},y,z) – V_x(x-\frac{ \Delta x}{2},y,z)\} \Delta y \Delta z \end{align}$$
ここでテイラー展開により
$$V_x(x \pm \frac{\Delta x}{2},y,z) \simeq V_x(x,y,z) \pm \frac{\partial V_{x}}{\partial x} \cdot \frac{\Delta x}{2}$$
となるので
$$\begin{align} (流出量)-(流入量) &= \{V_x(x,y,z) + \frac{\partial V_{x}}{\partial x} \cdot \frac{\Delta x}{2} – V_x(x,y,z) – \frac{\partial V_{x}}{\partial x} \cdot \frac{\Delta x}{2}\}\Delta y\Delta z \\ &=\frac{\partial V_{x}}{\partial x}\Delta x\Delta y\Delta z \end{align}$$
同様にy方向、z方向についても同様に考えて
$$(正味の流出量)= (\frac{\partial V_{x}}{\partial x}+ \frac{\partial V_{y}}{\partial y} + \frac{\partial V_{z}}{\partial z} )\Delta x\Delta y\Delta z $$
よって両辺を\(\Delta x\Delta y\Delta z\)で割ると単位体積当たりの正味の流出量が求まります。
$$(単位体積当たりの正味の流出量)= \frac{\partial V_{x}}{\partial x}+ \frac{\partial V_{y}}{\partial y} + \frac{\partial V_{z}}{\partial z} $$
つまりdivは「単位体積当たりの正味の流出量」を意味していることが分かりました。
divについて理解すると何が嬉しいのか?
divがどういうことを意味しているかについてはおおむね理解できたと思いますが、divを理解して何が嬉しいのか?という話になります。
簡単にいうと物理を表現するために当然のように出てくる記号だから覚えていないと出てくる数式が何を意味しているかが全く理解できないということになります。
逆に理解していれば、「なるほど!この式はこういうことを意味しているんだな!」と簡単に理解することができます。
例えば電磁気学でMaxwell方程式を学んだ場合、いきなり当然のように\(\mathrm{div}{\boldsymbol D} = \rho \)という数式がでてきます。
ここではMaxwell方程式についての説明は一旦置いておくとして、このときにdivについてただ定義を丸暗記していた場合は、この数式が物理的に何を意味しているのか全く理解できません。
また、丸暗記に頼ることになるでしょう。
そうすると物理って暗記することがどんどん増えてしんどいなということになりかねません。
一方でdivについて、それがどのような現象を表しているかを理解していれば、何か\({\boldsymbol D} \)のような湧き出しが \( \rho \) とイコールになるんだな、となんとなくイメージできると思います。
そうすれば、\({\boldsymbol D} \)と\( \rho \) が何を表しているのかを知るだけで、どのような現象を表しているかを簡単に理解することができます。
おすすめの参考書
物理数学の勉強におすすめの参考書を3冊ほど紹介しておきます。
最後に
物理を理解するときには、その数式がどのような現象を表しているかをイメージできるかが非常に重要になります。
このイメージができないと、物理ってただの式の羅列になってしまって全く面白く感じられず、勉強につまずいてしまいます。
一方で数式から現象をイメージできるようになれば、物理を学ぶのが楽しくなります。
一朝一夕で理解するのは難しいですが、少しずつ理解できるように頑張っていきましょう。