今回は単振動に外力を加えた運動である「強制振動」について考えていきます。
以前に単振動について考えましたが、強制振動は単振動に加えて質点に外力が加わる場合の運動になります。
今回の記事では、
- 強制振動の一般解
- 強制振動時にある条件で発生する「共鳴」と呼ばれる現象の特徴
- 共鳴条件下における運動の様子
を解説していきます。
強制振動
強制振動についてまず一般解を求めていくことになりますが、その前に強制振動のわかりやすい具体例について述べておきます。
個人的には、強制振動を一番イメージしやすいのはブランコに乗っている人を後ろから押している状態です。
ブランコに1人で乗って揺れている状態は単振動となっており、それに対して別の人が後ろからブランコを押して外力を加えているような状態です。
さて、それでは運動方程式を解いていき、強制振動の一般解を求めていきましょう!
強制振動の一般解
単振動に加えて外力$F(t)$がはたらいている強制振動の運動方程式は
\begin{eqnarray}
m\frac{d^2x}{dt^2}=-kx+F(t)\tag{1}
\end{eqnarray}
となります。
外力は時間の関数としており、さまざまな関数が考えられますが、ここでは簡単な例として振動している力、すなわち
\begin{eqnarray}
F(t)=F_0\cos\omega t\tag{2}
\end{eqnarray}
とします。
両辺を$m$で割り、$\omega_0^2=\frac{k}{m}$とおき式を整理すると、
\begin{eqnarray}
\frac{d^2x}{dt^2}+\omega_0^2x&=&\frac{F_0}{m}\cos\omega t\tag{3}
\end{eqnarray}
となります。これは2階非斉次(同次)線形微分方程式です。
この方程式の斉次微分方程式の一般解$x_1$、特解$x_2$とすると、一般解は$x=x_1+x_2$となります。
まず、斉次微分方程式の一般解$x_1$について考えていきましょう。
式(3)の右辺を0にした微分方程式の解を考えます。
これは単振動の運動方程式と同様の式の形をしており、任意の定数$A$、$B$を用いて、
\begin{eqnarray}
x_1=A\sin\omega_0 t+B\cos\omega_0 t\tag{4}
\end{eqnarray}
となります。
続いてこの微分方程式の特解$x_2$について考えます。
ばねについたおもりに対して前後に外力を加えれば、おもりは外力に応じた運動をするとよそうできます。
つまり方程式の特解は、
\begin{eqnarray}
x_2=C\cos\omega t\tag{5}
\end{eqnarray}
となります。$C$は定数です。
$x_2$を$t$で微分すると、$\frac{dx_2}{dt}=-\omega C\sin\omega t$、$\frac{d^2x_2}{dt^2}=-\omega^2 C\cos\omega t$となります。
これらを式(3)に代入し、整理して$C$を求めます。
\begin{eqnarray}
-\omega^2C\cos\omega t+\omega_0^2C\cos\omega t&=&\frac{F_0}{m}\cos\omega t\nonumber\\
(\omega_0^2-\omega^2)C\cos\omega t&=&\frac{F_0}{m}\cos\omega t\nonumber\\
C&=&\frac{F_0}{m(\omega_0^2-\omega^2)}\tag{6}
\end{eqnarray}
以上より、特解$x_2$は
\begin{eqnarray}
x_2=\frac{F_0}{m(\omega_0^2-\omega^2)}\cos\omega t\tag{7}
\end{eqnarray}
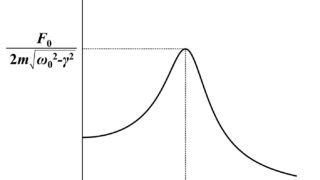
となります。$x_2$の振幅の大きさ$|C|$について見てみると、以下のようなグラフとなります。

$\omega$を$\omega_0$に限りなく近づけていくと振幅$|C|$は無限大に近づくことがわかります。
$\omega$は外力の角振動数、$\omega_0$は単振動の角振動数(固有角振動数という)を表し、これらの角振動数が近いほど大きな振動が発生するということです。
このような現象を「共鳴」とよびます。
以上より、$x$の一般解は
\begin{eqnarray}
x&=&x_1+x_2\nonumber\\
&=&A\sin\omega_0 t+B\cos\omega_0 t+\frac{F_0}{m(\omega_0^2-\omega^2)}\cos\omega t\tag{8}
\end{eqnarray}
となります。以上で$x$の一般解を求めることができました。
$\omega\to\omega_0$における運動(共鳴)
続いて具体的に振動の様子を見ていきます。
今、運動として気になるのは共鳴現象時にどのような運動と思います。
そこで$\omega\to\omega_0$のときの$x$について考えていきます。
初期条件を$t=0$、$x=0$、$dx/dt=0$とします。
まず、速度$dx/dt$を求めるために式(8)を微分します。
\begin{eqnarray}
\frac{dx}{dt}&=&A\omega_0\cos\omega_0 t-B\omega_0\sin\omega_0 t-\frac{F_0\omega}{m(\omega_0^2-\omega^2)}\sin\omega t\tag{9}
\end{eqnarray}
これで速度$dx/dt$の一般式が求まりました。それでは式(8)(9)に初期条件$t=0$、$x=0$、$dx/dt=0$を代入していきます。
\begin{eqnarray}
x(0)&=&B+\frac{F_0}{m(\omega_0^2-\omega^2)}\nonumber\\
&=&0\nonumber\\
\frac{dx(0)}{dt}&=&A\omega_0\nonumber\\
&=&0\nonumber
\end{eqnarray}
以上を計算して$A$、$B$を求めると、
\begin{eqnarray}
A&=&0\nonumber\\
B&=&-\frac{F_0}{m(\omega_0^2-\omega^2)}\nonumber
\end{eqnarray}
となります。求めた$A$、$B$を式(8)に代入して整理すると、
\begin{eqnarray}
x&=&-\frac{F_0}{m(\omega_0^2-\omega^2)}\cos\omega_0 t+\frac{F_0}{m(\omega_0^2-\omega^2)}\cos\omega t\nonumber\\
&=&\frac{F_0}{m(\omega_0^2-\omega^2)}(\cos\omega t-\cos\omega_0 t)\nonumber\\
&=&\frac{F_0}{m(\omega_0+\omega)(\omega_0-\omega)}\cdot{-2(\sin\frac{\omega+\omega_0}{2}t\sin\frac{\omega-\omega_0}{2}t)}\nonumber\\
&=&\frac{F_0t}{m(\omega_0+\omega)\frac{\omega-\omega_0}{2}t}\sin\frac{\omega+\omega_0}{2}t\sin\frac{\omega-\omega_0}{2}t\nonumber\\
&=&\frac{F_0t}{m(\omega_0+\omega)}\sin\frac{\omega+\omega_0}{2}t\frac{\sin\frac{\omega-\omega_0}{2}t}{\frac{\omega-\omega_0}{2}t}\tag{10}
\end{eqnarray}
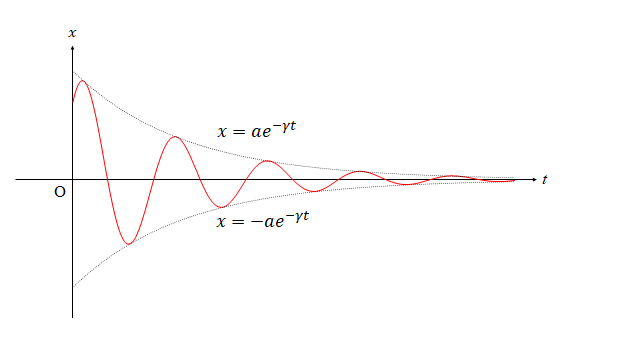
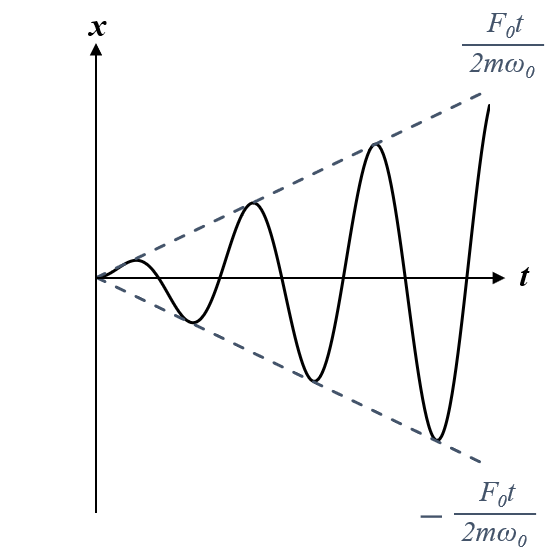
となります。ここで$\omega\to\omega_0$の極限をとると、
\begin{eqnarray}
\lim_{\omega \to \omega_0}x&=&\frac{F_0t}{2m\omega_0}\sin\omega_0t\tag{11}
\end{eqnarray}
となります。これをグラフ化すると以下のようになります。
このように$\omega$を$\omega_0$に限りなく近づけた場合、振動しながら時間が経つにつれて徐々に大きな振幅になるような運動をします。
複素表示を用いて強制振動を考える
ここまで計算したように、外力を$F(t)=F_0\cos\omega t$のように三角関数を用いて、運動方程式を立てて計算することは可能です。
しかし実際には外力を$F(t)=F_0e^{i\omega t}$とおき、複素数を用いて計算することも多いです。
なぜ指数関数を用いるのか?というと計算上取り扱いやすいからです。
$F(t)=F_0\cos \omega t$はオイラーの公式$e^{i\omega t}=\cos\omega t+i\sin\omega t$より、複素数$F(t)=F_0e^{i\omega t}$の実数部分となります。
つまり、$F(t)=F_0e^{i\omega t}$とおいて計算をすすめて、計算後に実数部分に注目すればよいわけです。
注意する点は実際に起こっている現象を知るためには実数部分をみる必要があることです。強制振動の運動方程式は、
\begin{eqnarray}
m\frac{d^2x}{dt^2}=-kx+F_0e^{i\omega t}\tag{12}
\end{eqnarray}
となります。両辺を$m$で割り、$\omega_0^2=\frac{k}{m}$とおき整理すると、
\begin{eqnarray}
\frac{d^2x}{dt^2}=-\omega_0^2x+\frac{F_0}{m}e^{i\omega t}\nonumber\\
\frac{d^2x}{dt^2}+\omega_0^2x=\frac{F_0}{m}e^{i\omega t}\tag{13}
\end{eqnarray}
となります。さて外力$F$が複素数ですので、$x$も当然複素数になることが予想できます。そこで$x=Ae^{i\omega t}$とおきます。
指数関数が便利な特徴の1つは微分するときに、指数を微分してかけるだけでよいところです。
$x$を微分すると$\frac{dx}{dt}=i\omega Ae^{i\omega t}$、$\frac{d^2x}{dt^2}=(i\omega)^2Ae^{i\omega t}$となります。
このように$e^{i\omega t}$の形が変わらないのが計算上便利なのです。
式(13)に$x=Ae^{i\omega t}$を代入して整理すると、
\begin{eqnarray}
(i\omega)^2Ae^{i\omega t}+\omega_0^2Ae^{i\omega t}&=&\frac{F_0}{m}e^{i\omega t}\nonumber\\ –
\omega^2Ae^{i\omega t}+\omega_0^2Ae^{i\omega t}&=&\frac{F_0}{m}e^{i\omega t}\nonumber\\
(\omega_0^2-\omega^2)Ae^{i\omega t}&=&\frac{F_0}{m}e^{i\omega t}\nonumber\\
A&=&\frac{F_0}{m(\omega_0^2-\omega^2)}\tag{14}
\end{eqnarray}
以上より、$x$は
\begin{eqnarray}
x=\frac{F_0}{m(\omega_0^2-\omega^2)}e^{i\omega t}\tag{15}
\end{eqnarray}
となります。この実数部分が実際に起こっている現象になります。
これは式(7)と一致しており、$F(t)=F_0\cos\omega t$で計算したときの特解と同様の値を求めることができました。
おすすめの参考書
力学の理解のためにおすすめの参考書を3冊ほど紹介しておきます。
「よくわかる初等力学」は図が豊富でイメージとして理解しやすい参考書となっています。計算過程も丁寧にかかれており初学者向けになっています。力学を勉強する1冊目の本としておすすめです。
「基幹講座物理学 力学」は理工系では通常学ばないような発展的な内容が含まれているのが特徴です。大学1年生向けに執筆したようですが、自学用の1冊目としてはおすすめしません。2冊目や副読本としては良い選択肢でしょう。
「ファインマン物理学」は有名なシリーズですべて良書です。ファインマン博士の個性的な人柄が読み取れる参考書になっています。読者に対する話かけがあり、講義を受けているような感覚で読み進めることができます。
最後に
本記事では、強制振動について解説しました。
強制振動において外力と単振動の角振動数が限りなく近づく条件で、その振幅は無限大に近づき、このような現象を「共鳴」と呼ばれます。
実際には摩擦力等のその他条件により振幅が無限大に大きくなることはありませんが、共鳴は力を効率よく使うために重要な現象となります。
Baby steps to Giant strides !