今回はベクトル解析で学ぶgrad(勾配;gradient)について説明していきます。
前回はベクトル解析で学ぶdiv(発散)について説明しましたが、それと同様に物理の教科書を理解するためには知っておくべき内容です。
個人的にはdivと比べるとgradのほうがイメージしやすいと考えていますが、定義を暗記するのではなく、イメージとして理解するように努めましょう。
grad(勾配)の定義とイメージ
gradの定義は次のようになります。
あるスカラー関数\( f=(x,y,z)\)とすると
$$\mathrm{grad}{f} = \frac{\partial f}{\partial x}\boldsymbol i+\frac{\partial f}{\partial y}\boldsymbol j + \frac{\partial f}{\partial z}\boldsymbol k $$
あるスカラー関数\(f\)に対してgradを計算することで
- 最大傾斜の方向
- 最大傾斜方向の傾き
を示すベクトルを導くことができます。
gradについて例は山をイメージするのがわかりやすいです。
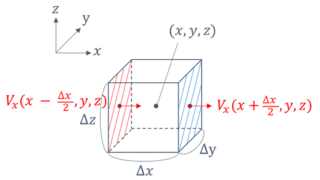
例えば下図のように山があり、ある位置を \((x,y,z)\) とします。

そしてこの山の表面の形状を示す関数を\(f\)とします。
ここでgradを計算することによって山の最大傾斜の方向と傾きがわかるということです。
gradが最大傾斜方向を示すことの証明
ここではgradが最大傾斜方向を示すことについて証明していきます。
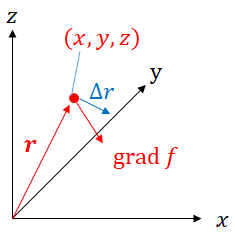
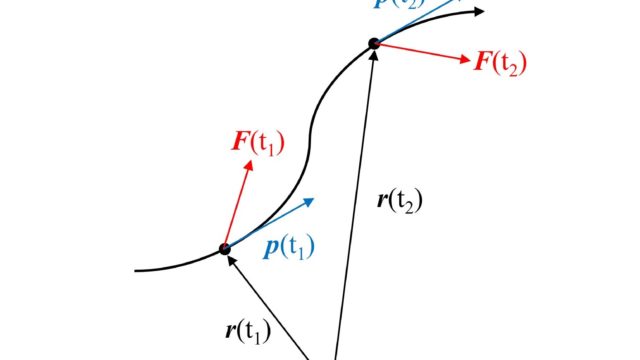
上図のように三次元空間上のある点を\((x,y,z)\)とし、その位置ベクトルを \( \boldsymbol r、 \boldsymbol r\) から微小変化したベクトルを \(\Delta \boldsymbol r\) とします。
すると\(f\)の微小な変化\(\Delta f\)は
$$\begin{align}\Delta f&=f(\boldsymbol r+\Delta \boldsymbol r)-f(\boldsymbol r)\\&=f(x+Δx, y+Δy, z+Δz)-f(x,y,z)\end{align}$$
ここで一次までのテイラー展開により
$$\begin{align}\Delta f &= f(x,y,z)+\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y+\frac{\partial f}{\partial z}\Delta z-f(x,y,z)\\ &=\mathrm{grad}f ・\Delta \boldsymbol r \\&=|\mathrm{grad} f||\Delta \boldsymbol r|\cos\theta \end{align}$$
ここで\(\Delta \boldsymbol r\)の微小変化の大きさをある値に固定し\(\Delta \boldsymbol r=\)一定とすると
\(\Delta f\)が最大となるのは\(\cos\theta=1\)
すなわち\(\theta=0\)のとき、\(\Delta f\)は最大となります。
つまり\(\Delta \boldsymbol r\)が\(\mathrm{grad} f\)の方向に進んだときに変化量は最大になります。
これにより \(\mathrm{grad} \) が最大傾斜方向を示すことが示されました。
おすすめの参考書
物理数学の勉強におすすめの参考書を3冊ほど紹介しておきます。
最後に
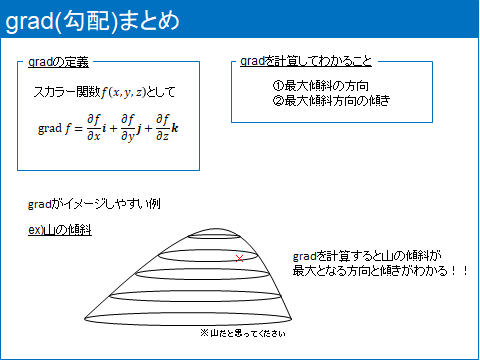
上図にまとめているように\(\mathrm{grad}\)の定義は
あるスカラー関数\( f=(x,y,z)\)とすると
$$\mathrm{grad}{f} = \frac{\partial f}{\partial x}\boldsymbol i+\frac{\partial f}{\partial y}\boldsymbol j + \frac{\partial f}{\partial z}\boldsymbol k $$
となり、gradを計算することで
- 最大傾斜方向
- 最大傾斜方向の傾き
がわかります。
ベクトル解析ではdiv、grad、rotの三種類の記号を勉強することになりますが、個人的にはこの中でgradが一番イメージしやすいと思います。
大学のテストを乗りきるだけであれば正直いうと理解していなくても定義を丸暗記して計算できるようにだけしておけば余裕で単位は取れます。
でも、 もしもあなたが物理を楽しみたいのであれば 、計算できるようにするだけでなく、数式を現象として理解できるようになることを目指しましょう!
Baby steps to Giant strides !