今回は単振動に外力と抵抗力を加えた運動である「減衰をふくむ強制振動」について考えていきます。
以前に減衰振動と強制振動について個別に運動を調べてきました。
今回は単振動にくわえて、減衰振動と強制振動の影響を同時に受ける質点の運動について考えていきます。
今回の記事では、
- 減衰をふくむ強制振動の一般解
- 振幅の角振動数依存性の図示
を解説していきます。
減衰をふくむ強制振動
強制振動でウォーミングアップは終わったので、続いてより現実的な現象に即した減衰のある強制振動について考えます。
強制振動と同様に外力$F(t)=F_0\cos\omega t$に加えて、摩擦のような抵抗力を付け加えます。
抵抗力は速度に比例するものとし、$F_f=-B\frac{dx}{dt}$とします。
外力は$F(t)=F_0e^{i\omega t}$として複素化して計算します。
すると運動方程式は、
\begin{eqnarray}
m\frac{d^2x}{dt^2}=-kx-B\frac{dx}{dt}+F_0e^{i\omega t}
\end{eqnarray}
となります。両辺を$m$で割り、$\omega_0^2=\frac{k}{m}$、$2\gamma=\frac{B}{m}$とおき整理すると、
\begin{eqnarray}
\frac{d^2x}{dt^2}=-\omega_0^2x-2\gamma\frac{dx}{dt}+\frac{F_0}{m}e^{i\omega t}\nonumber\\
\frac{d^2x}{dt^2}+2\gamma\frac{dx}{dt}+\omega_0^2x=\frac{F_0}{m}e^{i\omega t}
\end{eqnarray}
となります。これは2階非斉次(同次)線形微分方程式です。
この方程式の斉次微分方程式の一般解$x_1$、特解$x_2$とすると、一般解は$x=x_1+x_2$となります。
まず、斉次微分方程式の一般解$x_1$について考えていきましょう。
式(2)の右辺を0にした微分方程式の解を考えます。
これは以前【物理】減衰振動【力学】で計算しているのでそちらを確認してください。ここでは、特解$x_2$について考えていきます。
$x_2=Ae^{i\omega t}$とおくと、$\frac{dx_2}{dt}=i\omega Ae^{i\omega t}$、$\frac{d^2x_2}{dt^2}=(i\omega)^2Ae^{i\omega t}$となるので式(2)に代入して整理すると、
\begin{eqnarray}
(i\omega)^2Ae^{i\omega t}+2\gamma(i\omega)Ae^{i\omega t}+\omega_0^2Ae^{i\omega t}&=&\frac{F_0}{m}e^{i\omega t}\nonumber\\
-\omega^2Ae^{i\omega t}+2i\gamma\omega Ae^{i\omega t}+\omega_0^2Ae^{i\omega t}&=&\frac{F_0}{m}e^{i\omega t}\nonumber\\
(\omega_0^2-\omega^2+2i\gamma\omega)Ae^{i\omega t}&=&\frac{F_0}{m}e^{i\omega t}\nonumber\\
A=\frac{F_0}{m(\omega_0^2-\omega^2+2i\gamma\omega)}
\end{eqnarray}
となります。これにより$A$は強制振動と同様に$F_0$に係数をかけたものであることがわかりました。
ここからもう少し運動を考察しやすいように式を変形していきます。まずこの係数を$R$とおきます。すなわち、
\begin{eqnarray}
R&=&\frac{1}{m(\omega_0^2-\omega^2+2i\gamma\omega)}
\end{eqnarray}
とおきます。これにより$A=RF_0$となります。
係数$R$は複素数なので$R=p+iq$の形でかき表され、さらにこの極形式である$R=|z|e^{i\phi}$でかけます。すなわち、
\begin{eqnarray}
R&=&\frac{1}{m(\omega_0^2-\omega^2+2i\gamma\omega)}=|z|e^{i\phi}
\end{eqnarray}
とかけるはずです。それでは$z$を求めていきます。
複素数の絶対値の二乗は、その複素数に対して共役な複素数をかけたものです。よって$z^2$は
\begin{eqnarray}
z^2&=&\frac{1}{m(\omega_0^2-\omega^2+2i\gamma\omega)}\times\frac{1}{m(\omega_0^2-\omega^2-2i\gamma\omega)}\nonumber\\
&=&\frac{1}{m^2\{(\omega_0^2-\omega^2)^2+4\gamma^2\omega^2\}}
\end{eqnarray}
となります。よって$|z|$は、
\begin{eqnarray}
|z|&=&\frac{1}{m\sqrt{(\omega_0^2-\omega^2)^2+4\gamma^2\omega^2}}
\end{eqnarray}
となります。続いて$\phi$を求めます。式(5)の逆数をとると、
\begin{eqnarray}
\frac{1}{R}&=&m(\omega_0^2-\omega^2+2i\gamma\omega)=\frac{1}{z}e^{-i\phi}
\end{eqnarray}
となります。ここでオイラーの公式より$e^{-i\phi}=\cos\phi-i\sin\phi$となるので式(11)より、
\begin{eqnarray}
m(\omega_0^2-\omega^2+2i\gamma\omega)=\frac{1}{z}
\cos\phi-i\sin\phi)
\end{eqnarray}
となります。この両辺の実部と虚部を比較すると、
\begin{eqnarray}
\cos\phi&=&mz(\omega_0^2-\omega^2)\nonumber\\
\sin\phi&=&-2mz\gamma\omega\nonumber
\end{eqnarray}
となるので、
\begin{eqnarray}
\tan\phi&=&\frac{\sin\phi}{\cos\phi}\nonumber\\
&=&-\frac{2mz\gamma\omega}{mz(\omega_0^2-\omega^2)}\nonumber\\
&=&-\frac{2\gamma\omega}{\omega_0^2-\omega^2}
\end{eqnarray}
となります。以上により特解$x_2$は
\begin{eqnarray}
x_2&=&Ae^{i\omega t}\nonumber\\
&=&RF_0e^{i\omega t}\nonumber\\
&=&|z|e^{i\phi}F_0e^{i\omega t}\nonumber\\
&=&\frac{F_0e^{i(\omega t+\phi)}}{m\sqrt{(\omega_0^2-\omega^2)^2+4\gamma^2\omega^2}}
\end{eqnarray}
となります。この実数部分が運動の様子を表します。
オイラーの公式より$e^{i(\omega t+\phi)}=\cos(\omega t+\phi)+i\sin(\omega t+\phi)$となるので、$x_2$の実数部分は、
\begin{eqnarray}
x_2&=&\frac{F_0\cos(\omega t+\phi)}{m\sqrt{(\omega_0^2-\omega^2)^2+4\gamma^2\omega^2}}
\end{eqnarray}
となります。以上で減衰のある強制振動の一般解$x=x_1+x_2$を求めることができました。
振幅の大きさ$|x_2|$の$\omega$依存性
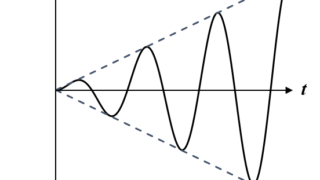
続いて運動の様子を知りたいのですが、以前の減衰振動で$x_1$の運動の様子を図示しています。
そちらを見ると、時間がたつと速やかに振幅が減衰することがわかります。
つまり十分に時間がたつと$x_1$はほぼ0になってしまい、定常的に起こる運動は$x=x_2$になります。
そこで$x=x_2$の運動の様子を見ていきます。
さてこの運動の様子をもう少し詳しく見ていきましょう。
まず角周波数$\omega$に対する$x_2$の振幅$|x_2|$の変化を見ていきます。
$|x_2|$の極値を調べるために平方完成で分母を整理すると、
\begin{eqnarray}
|x_2|&=&\frac{F_0}{m\sqrt{(\omega_0^2-\omega^2)^2+4\gamma^2\omega^2}}\nonumber\\
&=&\frac{F_0}{m\sqrt{\omega_0^4-2\omega_0^2\omega^2+\omega^4+4\gamma^2\omega^2}}\nonumber\\
&=&\frac{F_0}{m\sqrt{\omega^4-2(\omega_0^2-2\gamma^2)\omega^2+\omega_0^4}}\nonumber\\
&=&\frac{F_0}{m\sqrt{\{\omega^2-(\omega_0^2-2\gamma^2)\}^2-(\omega_0^2-2\gamma^2)^2+\omega_0^4}}\nonumber\\
&=&\frac{F_0}{m\sqrt{\{\omega^2-(\omega_0^2-2\gamma^2)\}^2+4\gamma^2(\omega_0^2-\gamma^2)}}
\end{eqnarray}
となります。ここで、$\omega_0^2-2\gamma^2\geqq0$と$\omega_0^2-2\gamma^2<0$で場合わけします。ただし、$\omega_0\geqq0$、$\gamma\geqq0$とします。
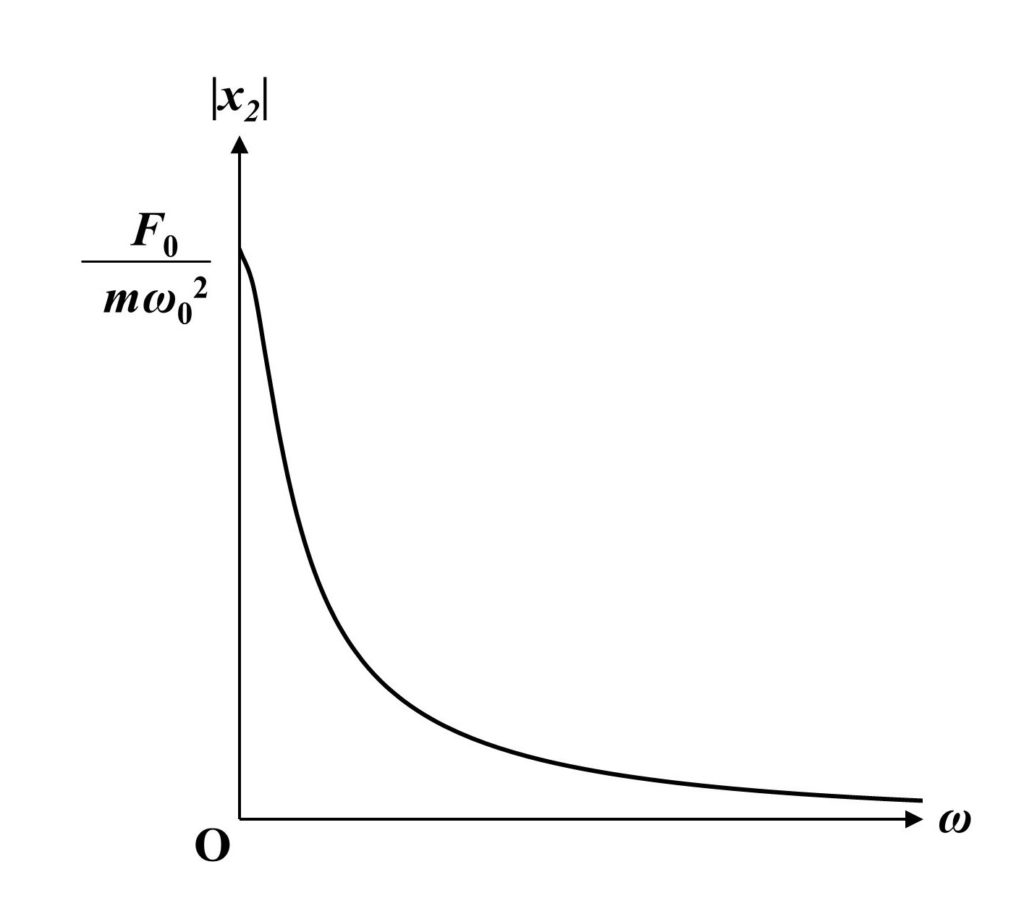
(1)$\gamma\leqq\omega_0/\sqrt{2}$のとき
$\omega_0^2-2\gamma^2\geqq0$すなわち$\gamma\leqq\frac{\omega_0}{\sqrt{2}}$のときについて考えます。
$\omega=\sqrt{\omega_0^2-2\gamma^2}$で$|x_2|$は最大値となります。
つまり共鳴条件は$\omega=\sqrt{\omega_0^2-2\gamma^2}$となります。
角振動数$\omega$によって振幅の大きさ$|x_2|$はどのように変化するかを以下に図示します。

$\gamma$は抵抗力の大きさを意味する値を表していますが、$\gamma\approx0$のとき、すなわち抵抗力が$0$に近いとき、共鳴条件は$\omega\approx\omega_0$となります。
これは今回のように抵抗力がない強制振動の共鳴条件と一致していることがわかります。(強制振動についてはこちら)
(2)$\gamma>\omega_0/\sqrt{2}$のとき
$\omega_0^2-2\gamma^2<0$すなわち$\gamma>\frac{\omega_0}{\sqrt{2}}$のときについて考えます。
$|x_2|$の分母は$\omega$が増加するにしたがって単調増加することがわかります。
つまり$|x_2|$は$\omega$の増大によって単調減少することがわかります。
角振動数$\omega$によって振幅の大きさ$|x_2|$はどのように変化するかを以下に図示します。
この場合、$\omega$が増加すると急激に振幅の大きさ$|x_2|$が小さくなる傾向があることが見て取れます。
おすすめの参考書
力学の理解のためにおすすめの参考書を3冊ほど紹介しておきます。
「考える力学」は丁寧に書かれており、初学者向けの参考書となっています。力学で用いる数学についても詳しく解説されており、力学を勉強する1冊目の本としておすすめです。
「基幹講座物理学 力学」は理工系では通常学ばないような発展的な内容が含まれているのが特徴です。大学1年生向けに執筆したようですが、自学用の1冊目としてはおすすめしません。2冊目や副読本としては良い選択肢でしょう。
「ファインマン物理学」は有名なシリーズですべて良書です。ファインマン博士の個性的な人柄が読み取れる参考書になっています。読者に対する話かけがあり、講義を受けているような感覚で読み進めることができます。
最後に
本記事では、減衰をふくむ強制振動について解説しました。
強制振動の場合は共鳴条件で振幅が無限大に発散しましたが、減衰をふくむ強制振動の場合には共鳴条件においても発散せずに最大振幅がある値に決まりました。
減衰をふくむ強制振動について考えることで、普段の生活の中でより現実的な世界の運動について考えることができました。
Baby steps to Giant strides !