今回は運動方程式から「力学的エネルギー保存則」を導いていきます。
前回は運動量保存則について解説しました。今回の力学的エネルギー保存則は、運動量保存則に引き続き第2の保存則となります。
今回は、
- 仕事について
- 仕事と運動エネルギーについて
- 仕事とポテンシャルエネルギーについて
- 力学的エネルギー保存則の導出
について解説していきます。
仕事
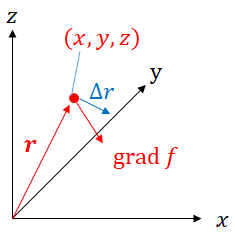
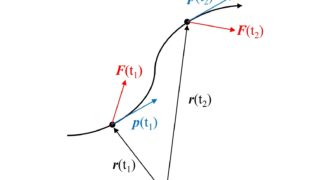
3次元空間において、力$\boldsymbol{F}$を受けながら微小な距離$d\boldsymbol{r}$だけ移動したときの仕事$dW$は力と変位の内積
\begin{eqnarray}
dW=\boldsymbol{F}\cdot d\boldsymbol{r}\tag{1}
\end{eqnarray}
で与えられます。$dW$は微小な距離$d\boldsymbol{r}$の間の仕事ですが、質点が力$\boldsymbol{F}(\boldsymbol{r})$を受けながら点Aから点Bまで移動する間の仕事$W$は、点Aから点Bまで移動する経路を$\rm{C}$とすると、経路$\rm{C}$の各微小区間の仕事の総和で与えられるので、
\begin{eqnarray}
W=\int_{\rm{C}}\boldsymbol{F}(\boldsymbol{r})\cdot d\boldsymbol{r}\tag{2}
\end{eqnarray}
となります。このように2点をつなぐ経路にそった積分のことを線積分といいます。一般に、線積分は経路の選択に依存します。つまり上式でいうならば仕事$W$は経路$\rm{C}$に依存します。ただし、力$\boldsymbol{F}(\boldsymbol{r})$が保存力の場合には仕事$W$が経路$\rm{C}$によりません。つまり力$\boldsymbol{F}(\boldsymbol{r})$が保存力の場合、仕事$W$は経路によらず点Aと点Bにおける運動によって決まり、
\begin{eqnarray}
W=\int_{\boldsymbol{r}_A}^{\boldsymbol{r}_B}\boldsymbol{F}(\boldsymbol{r})\cdot d\boldsymbol{r}\tag{3}
\end{eqnarray}
となります。$\boldsymbol{r}_A$、$\boldsymbol{r}_B$は点A、Bの位置を表します。
仕事と運動エネルギーの関係
質点の軌道上に点Aと点Bをとり、AB間の運動について考えます。質点が点A,Bにあるときの時刻を$t_A,t_B$とします。運動方程式$m\frac{d\boldsymbol{v}}{dt}=\boldsymbol{F}(\boldsymbol{r})$の両辺に速度$\boldsymbol{v}$の内積をとり、時刻$t_A\sim t_B$まで積分すると、
\begin{eqnarray}
\int_{t_A}^{t_B} m\frac{d\boldsymbol{v}}{dt}\cdot\boldsymbol{v}dt=\int_{t_A}^{t_B} \boldsymbol{F}(\boldsymbol{r})\cdot\boldsymbol{v}dt\tag{4}
\end{eqnarray}
となります。ここで、
\begin{eqnarray}
\frac{d}{dt}\left(\frac{1}{2}m\boldsymbol{v}^2\right)&=&\frac{m}{2}\frac{d}{dt}\left(\boldsymbol{v}\cdot\boldsymbol{v}\right)\nonumber\\
&=&\frac{m}{2}\left(\frac{d\boldsymbol{v}}{dt}\cdot\boldsymbol{v}+\boldsymbol{v}\cdot\frac{d\boldsymbol{v}}{dt}\right)\nonumber\\
&=&m\frac{d\boldsymbol{v}}{dt}\cdot\boldsymbol{v}\tag{5}
\end{eqnarray}
となるので式(4)の左辺は、
\begin{eqnarray}
\int_{t_A}^{t_B} m\frac{d\boldsymbol{v}}{dt}\cdot\boldsymbol{v}dt&=&\int_{t_A}^{t_B} \frac{d}{dt}\left(\frac{1}{2}m\boldsymbol{v}^2\right)dt\nonumber\\
&=&\frac{1}{2}m\boldsymbol{v}_B^2-\frac{1}{2}m\boldsymbol{v}_A^2\tag{6}
\end{eqnarray}
となります。ただし$\boldsymbol{v}_A,\boldsymbol{v}_B$は、点A,Bの速度となります。また、式(4)の右辺は、
\begin{eqnarray}
\int_{t_A}^{t_B} \boldsymbol{F}(\boldsymbol{r})\cdot\boldsymbol{v}dt&=&\int_{t_A}^{t_B} \boldsymbol{F}(\boldsymbol{r})\cdot\frac{d\boldsymbol{r}}{dt}dt\nonumber\\
&=&\int_{\boldsymbol{r}_A}^{\boldsymbol{r}_B} \boldsymbol{F}(\boldsymbol{r})\cdot d\boldsymbol{r}\tag{7}
\end{eqnarray}
となります。ただし$\boldsymbol{r}_A,\boldsymbol{r}_B$は、点A,Bの位置となります。以上より式(4)は、
\begin{eqnarray}
\frac{1}{2}m\boldsymbol{v}_B^2-\frac{1}{2}m\boldsymbol{v}_A^2=\int_{\boldsymbol{r}_A}^{\boldsymbol{r}_B} \boldsymbol{F}(\boldsymbol{r})\cdot d\boldsymbol{r}\tag{8}
\end{eqnarray}
と書き換えられます。式(8)の右辺は点A,Bの$\frac{1}{2}mv^2$という量の変化量を表しています。式(8)の右辺は力$\boldsymbol{F}(\boldsymbol{r})$を受けながら点Aから点Bまで移動する間の仕事を表しています。ここで、
\begin{eqnarray}
K=\frac{1}{2}mv^2\tag{9}
\end{eqnarray}
と定義し、質点がもつ運動エネルギーといいます。以上より、式(8)は、
\begin{eqnarray}
K_B-K_A&=&\int_{\boldsymbol{r}_A}^{\boldsymbol{r}_B} \boldsymbol{F}(\boldsymbol{r})\cdot d\boldsymbol{r}\tag{10}
\end{eqnarray}
と表されます。この式は、質点が点Aから点Bまで運動する間の運動エネルギーの増加量は質点にはたらく力がする仕事に等しいことを示しています。
仕事とポテンシャルエネルギーの関係
保存力$\boldsymbol{F}(\boldsymbol{r})$に対して任意の基準点$\boldsymbol{r}_0$を定め、他の任意の点を$\boldsymbol{r}$とすると、
\begin{eqnarray}
U(\boldsymbol{r})=-\int_{\boldsymbol{r}_0}^{\boldsymbol{r}}\boldsymbol{F}(\boldsymbol{r})\cdot d\boldsymbol{r}\tag{11}
\end{eqnarray}
と定義し、これを$\boldsymbol{r}_0$を基準にしたときのポテンシャルエネルギーといいます。質点が点Aと点Bにあるときのポテンシャルエネルギーの差は、
\begin{eqnarray}
U(\boldsymbol{r}_B)-U(\boldsymbol{r}_A)&=&-\int_{\boldsymbol{r}_0}^{\boldsymbol{r_B}}\boldsymbol{F}(\boldsymbol{r})\cdot d\boldsymbol{r}-\left(-\int_{\boldsymbol{r}_0}^{\boldsymbol{r_A}}\boldsymbol{F}(\boldsymbol{r})\cdot d\boldsymbol{r}\right)\nonumber\\
&=&-\int_{\boldsymbol{r}_A}^{\boldsymbol{r_B}}\boldsymbol{F}(\boldsymbol{r})\cdot d\boldsymbol{r}\tag{12}
\end{eqnarray}
と表されます。この式は、点Aと点Bのポテンシャルエネルギーの差は、負号をつけた質点にはたらく力がする仕事に等しいことを示しています。ポテンシャルエネルギーの差は基準点$\boldsymbol{r}_0$によらず決まるので、基準点$\boldsymbol{r}_0$は任意に決めても問題ありません。通常は式がシンプルになるように定めます。
力学的エネルギー保存則
質点が保存力$\boldsymbol{F}(\boldsymbol{r})$を受けながら点Aから点Bに移動するとき、ここまで求めてきた、仕事と運動エネルギーの関係式(式(10))、仕事とポテンシャルエネルギーの関係式(式(12))、
\begin{eqnarray}
K_B-K_A&=\int_{\boldsymbol{r}_A}^{\boldsymbol{r}_B} \boldsymbol{F}(\boldsymbol{r})\cdot d\boldsymbol{r}\tag{10}\\
U(\boldsymbol{r}_B)-U(\boldsymbol{r}_A)&=-\int_{\boldsymbol{r}_A}^{\boldsymbol{r_B}}\boldsymbol{F}(\boldsymbol{r})\cdot d\boldsymbol{r}\tag{12}
\end{eqnarray}
が成り立ちます。これらの式より運動エネルギーとポテンシャルエネルギーの関係式は、
\begin{eqnarray}
K_B-K_A=-U(\boldsymbol{r}_B)+U(\boldsymbol{r}_A)\tag{13}
\end{eqnarray}
となります。ここで、点Aに関する量を左辺、点Bに関する量を右辺に移項して整理すると、
\begin{eqnarray}
K_A+U(\boldsymbol{r}_A)=K_B+U(\boldsymbol{r}_B)\tag{14}
\end{eqnarray}
となります。ここで、
\begin{eqnarray}
E=K+U(\boldsymbol{r})=\frac{1}{2}mv^2+U(\boldsymbol{r})\tag{15}
\end{eqnarray}
と定義すると、$E$は力学的エネルギーと呼ばれ、運動エネルギーとポテンシャルエネルギーの和を示します。定義式(15)により、式(14)は、
\begin{eqnarray}
E_A=E_B\tag{16}
\end{eqnarray}
となり、点Aから点Bに移動しても力学的エネルギー$E$は一定であることがわかります。つまり、保存力のみを受けながら運動する質点の運動において、力学的エネルギーは常に一定であることを表しています。これを力学的エネルギー保存則といいます。
おすすめの参考書
力学の理解のためにおすすめの参考書を2冊ほど紹介しておきます。
「考える力学」は丁寧に書かれており、初学者向けの参考書となっています。力学で用いる数学についても詳しく解説されており、力学を勉強する1冊目の本としておすすめです。
「基幹講座物理学 力学」は理工系では通常学ばないような発展的な内容が含まれているのが特徴です。大学1年生向けに執筆したようですが、自学用の1冊目としてはおすすめしません。2冊目や副読本としては良い選択肢でしょう。
最後に
今回は「力学的エネルギー保存則」について解説しました。
質点が力$\boldsymbol{F}(\boldsymbol{r})$を受けながら点Aから点Bまで移動するとき、仕事と運動エネルギー$K$の関係は、
\begin{eqnarray}
K_B-K_A&=&\int_{\boldsymbol{r}_A}^{\boldsymbol{r}_B} \boldsymbol{F}(\boldsymbol{r})\cdot d\boldsymbol{r}
\end{eqnarray}
となり、仕事とポテンシャルエネルギー$U(\boldsymbol{r})$の関係は
\begin{eqnarray}
U(\boldsymbol{r}_B)-U(\boldsymbol{r}_A)=-\int_{\boldsymbol{r}_A}^{\boldsymbol{r_B}}\boldsymbol{F}(\boldsymbol{r})\cdot d\boldsymbol{r}
\end{eqnarray}
となり、これらの式から
\begin{eqnarray}
K_A+U(\boldsymbol{r}_A)=K_B+U(\boldsymbol{r}_B)
\end{eqnarray}
が導かれます。運動エネルギーとポテンシャルエネルギーの和は力学的エネルギーとよばれ、$E$で表され、点Aから点Bに移動しても力学的エネルギー$E$は一定であることがわかります。
今後は3つ目の保存則である角運動量保存則について解説しようと思います。
Baby steps to Giant strides !