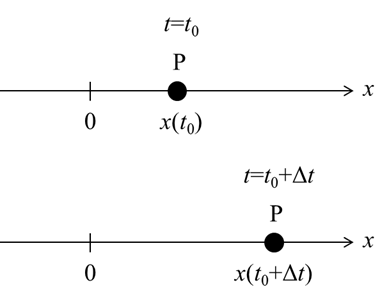
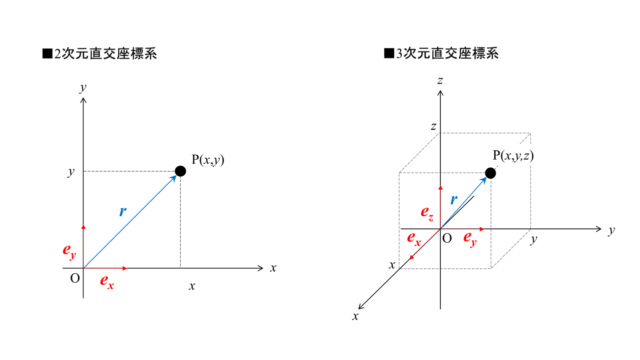
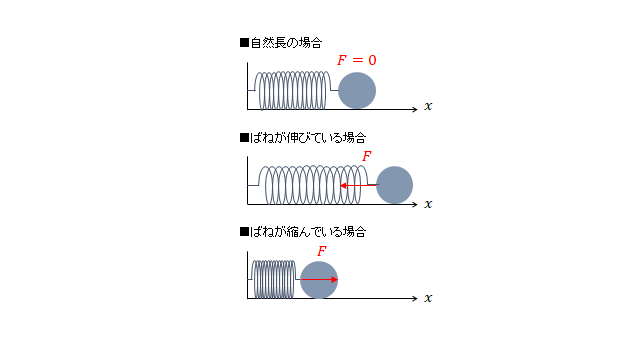
今回は「角運動量と力のモーメント」の関係や「運動量保存則」について考えていきます。
ニュートン力学においては運動をしていても変化しない量があり、保存則として「運動量保存則」「力学的エネルギー保存則」「角運動量保存則」があります。
今回の記事では、
- 角運動量と力のモーメントについて
- 角運動量保存則
- ケプラーの第2法則(面積一定の法則)
について解説していきます。
角運動量と力のモーメント
運動方程式$\boldsymbol{F}=m\frac{d^2\boldsymbol{r}}{dt^2}$は運動量$\boldsymbol{p}=m\boldsymbol{v}=m\frac{d\boldsymbol{r}}{dt}$を用いて、
\begin{eqnarray}
\boldsymbol{F}=\frac{d\boldsymbol{p}}{dt}\tag{1}
\end{eqnarray}
と書くことができます。この式に対して両辺と位置ベクトル$\boldsymbol{r}$の外積をとると、
\begin{eqnarray}
\boldsymbol{r}\times\boldsymbol{F}&=&\boldsymbol{r}\times\frac{d\boldsymbol{p}}{dt}\tag{2}
\end{eqnarray}となります。ここで、
\begin{eqnarray}
\frac{d}{dt}(\boldsymbol{r}\times\boldsymbol{p})&=&\frac{d\boldsymbol{r}}{dt}\times\boldsymbol{p}+\boldsymbol{r}\times\frac{d\boldsymbol{p}}{dt}\tag{3}
\end{eqnarray}
となりますが、右辺の第1項について${d\boldsymbol{r}}/{dt}=\boldsymbol{v}$、$\boldsymbol{p}=m\boldsymbol{v}$となるので、$d\boldsymbol{r}/dt$と$\boldsymbol{p}$は平行です。平行な量の外積は$0$となるので右辺の第1項は
\begin{eqnarray}
\frac{d\boldsymbol{r}}{dt}\times\boldsymbol{p}=0\tag{4}
\end{eqnarray}
となります。つまり式(3)は、
\begin{eqnarray}
\frac{d}{dt}(\boldsymbol{r}\times\boldsymbol{p})&=&\boldsymbol{r}\times\frac{d\boldsymbol{p}}{dt}\tag{5}
\end{eqnarray}
となります。以上より、式(2)は式(5)を用いて、
\begin{eqnarray}
\boldsymbol{r}\times\boldsymbol{F}&=&\frac{d}{dt}(\boldsymbol{r}\times\boldsymbol{p})\tag{6}
\end{eqnarray}
となります。この式の左辺の$\boldsymbol{r}\times\boldsymbol{F}$を原点に関する力のモーメントといい、$\boldsymbol{N}$で表します。
高校で習ったと思いますが、力のモーメントはある点のまわりに物体を回転させようとする力の作用を表す量です。
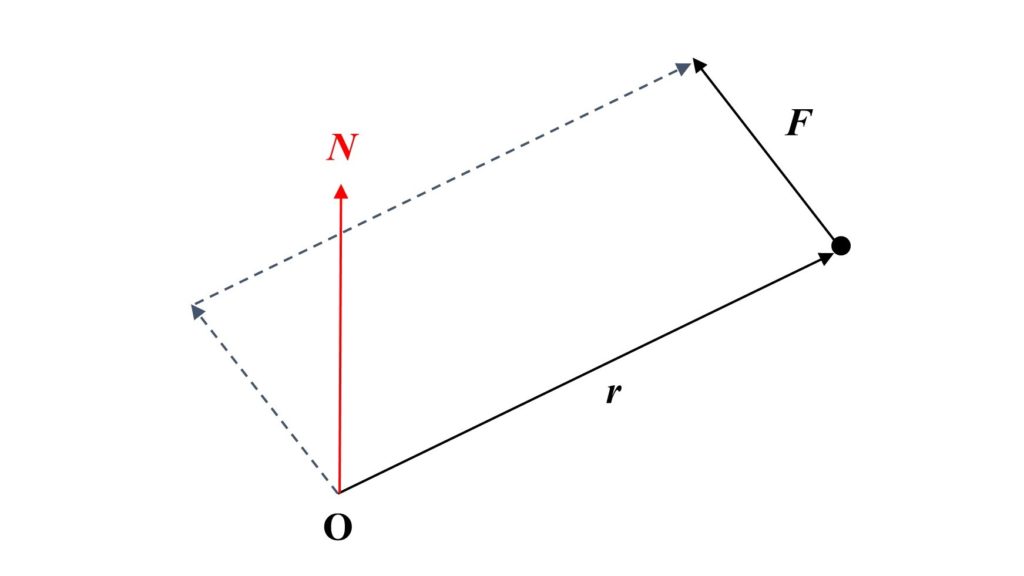
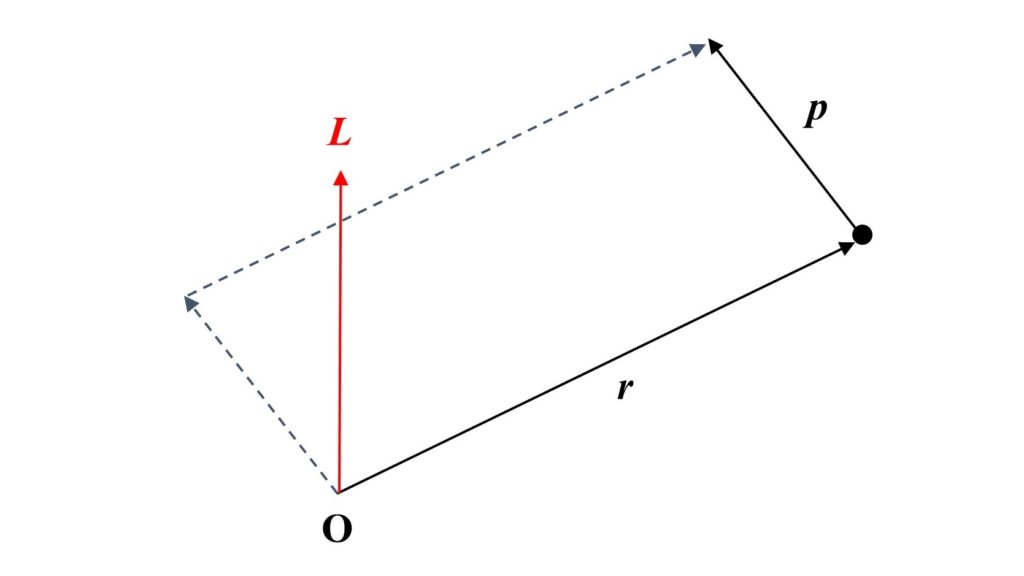
また、この式の右辺の$\boldsymbol{r}\times\boldsymbol{p}$を角運動量といい、$\boldsymbol{L}$で表します。以上より式(2)は、
\begin{eqnarray}
\boldsymbol{N}&=&\frac{d\boldsymbol{L}}{dt}\tag{7}
\end{eqnarray}
となり、質点にはたらく力のモーメントは、運動する質点の角運動量の時間変化に等しいことを表しています。
角運動量保存則
式(7)の右辺は角運動量の時間微分になっていますが、角運動量の時間微分が$0$のときに$\boldsymbol{L}=$一定となり角運動量が保存されます。
つまり式(7)において$N=0$のとき$d\boldsymbol{L}/dt=0$となり、
\begin{eqnarray}
\boldsymbol{L}=一定\tag{8}
\end{eqnarray}
であるから角運動量保存則が成り立つことがわかります。
ここで質点にどのような力が働けば、力のモーメント$\boldsymbol{N}=0$になるか考えます。
$\boldsymbol{N}=\boldsymbol{r}\times\boldsymbol{F}$なので、1つは$\boldsymbol{F}=0$のときに$\boldsymbol{N}=0$となります。
また、$\boldsymbol{r}//\boldsymbol{F}$のとき、$\boldsymbol{N}=0$となることがわかります。
すなわち、質点に対して万有引力のような中心力がはたらく場合に$\boldsymbol{N}=0$となり、角運動量保存則が成り立ちます。
角運動量保存則が成り立つとき、$\boldsymbol{L}=$一定なので、$\boldsymbol{L}$の方向が一定に保たれます。
$\boldsymbol{L}=\boldsymbol{r}\times\boldsymbol{p}$なので、角運動量$\boldsymbol{L}$は、位置ベクトル$\boldsymbol{r}$と運動量$\boldsymbol{p}(=m\boldsymbol{v})$の両方に垂直となります。
つまり、角運動量保存則が成り立つ($\boldsymbol{L}=$一定)とき、$\boldsymbol{r}$と$\boldsymbol{v}$を含む平面が一定に保たれ、質点の軌道はその平面上内であることを意味します。
ケプラーの第2法則(面積速度一定の法則)
角運動量保存則の有名な例として、ケプラーの第2法則である「面積速度一定の法則」があります。
この法則について説明していきます。
原点$\rm{O}$から中心力を受けて運動している質点$\rm{P}$について考えます。
質点の速度を$\boldsymbol{v}$とすると、微小時間$dt$で進む距離は$\boldsymbol{v}dt$となります。
動径$\rm{OP}$が微小時間$dt$の間に掃過する面積が下図の斜線部分となります。
また下図のように質点$\rm{P}$の位置ベクトル$\boldsymbol{r}$と運動量$\boldsymbol{p}$のなす角を$\theta$とします。
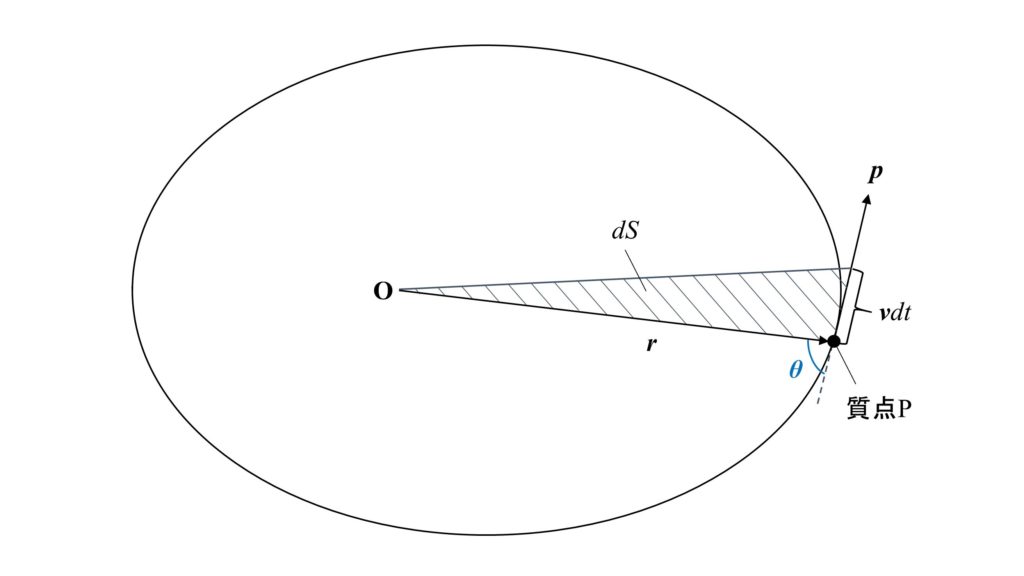
この面積を$dS$とすると、
\begin{eqnarray}
dS=\frac{1}{2}rvdt\sin\theta\tag{9}
\end{eqnarray}
となります。面積速度は$dS$を$dt$で割った、
\begin{eqnarray}
\frac{dS}{dt}=\frac{1}{2}rv\sin\theta\tag{10}
\end{eqnarray}
となります。一方でこの質点$\rm{P}$の角運動量の大きさ$|\boldsymbol{L}|$は、
\begin{eqnarray}
|\boldsymbol{L}|&=&|\boldsymbol{r}\times\boldsymbol{p}|\nonumber\\
&=&rp\sin\theta\nonumber\\
&=&rmv\sin\theta\nonumber\\
&=&2m\frac{dS}{dt}\tag{11}
\end{eqnarray}
となることがわかります。角運動量保存則により、中心力を受けて運動する質点$\rm{P}$の角運動量$\boldsymbol{L}$は一定なので、面積速度$dS/dt$は一定になります。
最後に
ケプラーの第2法則はそもそもケプラーが実験データから発見し、後々にニュートンが理論的に証明しています。
惑星に関する実験データからこの法則を見出したケプラーもすごいですが、ニュートン力学と結び付けて理論的に証明したニュートンもすごいですよね。
Baby steps to Giant strides !