今回は2次元・3次元空間の位置・速度・加速度について説明します。
前回は1次元の位置・速度・加速度について説明しました。
1次元空間における位置・速度・加速度についてまとめておきましょう。
ある点の位置\(x\)、速度\(v\)、加速度\(a\)とすると
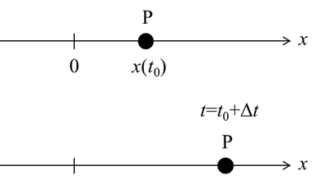
$$\begin{align} v &=\lim_{\Delta t \rightarrow 0} \frac{x(t_0 +\Delta t)-x(t_0)}{\Delta t} =\frac{d x}{d t}\\ a &=\lim_{\Delta t \rightarrow 0} \frac{v(t_0 +\Delta t)-v(t_0)}{\Delta t} =\frac{d v}{d t}\end{align}$$
また、速度・加速度は次のように表すこともあります。
$$\begin{align}v &=\dot x=\frac{dx}{dt} \\a &= \dot v=\frac{dv}{dt} =\ddot x = \frac{d^2 x}{dt^2}\end{align} $$
1次元空間においては位置と時間の関係さえわかれば、速度・加速度を求めることができることがわかりました。
今回は2次元・3次元に拡張して考えていきます。
2次元・3次元空間における位置・速度・加速度
2次元・3次元空間の位置
2次元・3次元空間における点の運動について考えていきます。
点の運動は時間とともに位置がどう変化するかによって記述されます。
この位置を数値的に取りあつかうために座標系を導入します。
代表的な座標系として
- 直交座標系
- 極座標系
の2種類があります。
ただし、ここでは直交座標系で考えていくことにします。
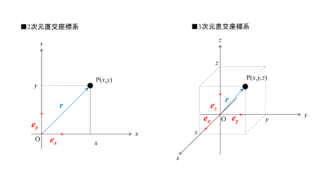
2次元直交座標系では\(x\)軸と\(y\)軸が互いに直交して交わり、3次元直交座標系では\(x\)軸、\(y\)軸、\(z\)軸が互いに直交して交わります。
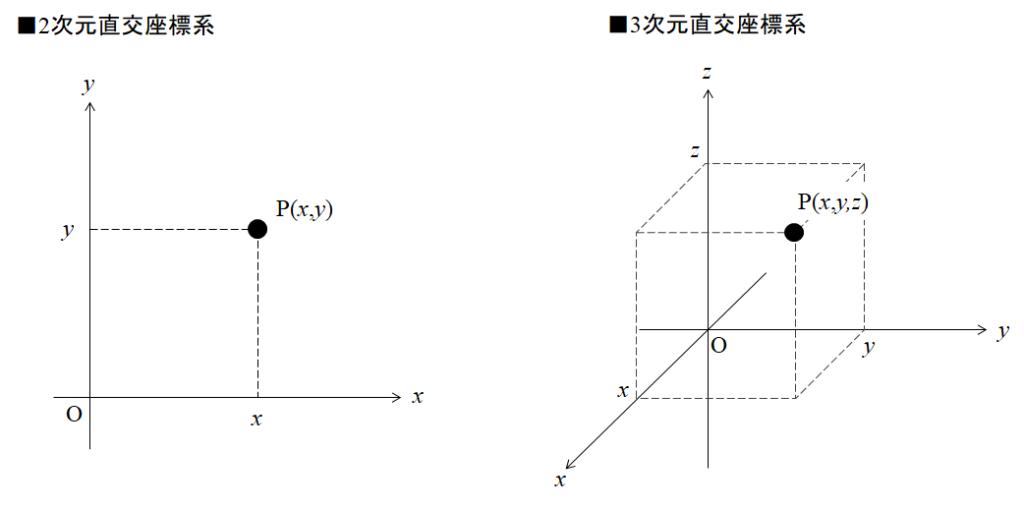
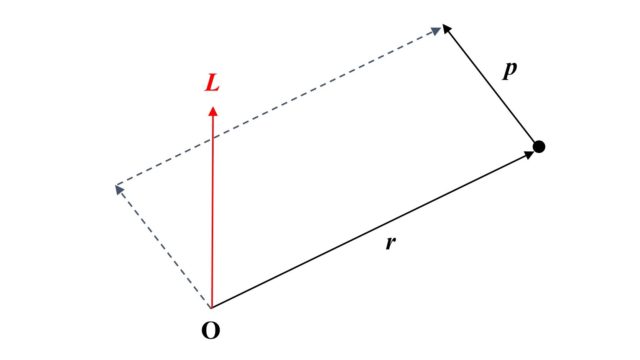
点の位置は上記の点Pのように座標を用いて表してもよいが、位置ベクトルを用いて表すと便利なことも多いです。
点Pの位置ベクトルとは、原点Oから点Pまでの移動を表すベクトル(下図青矢印)のことです。位置ベクトルは\(\boldsymbol r\)と表すことが多いです。
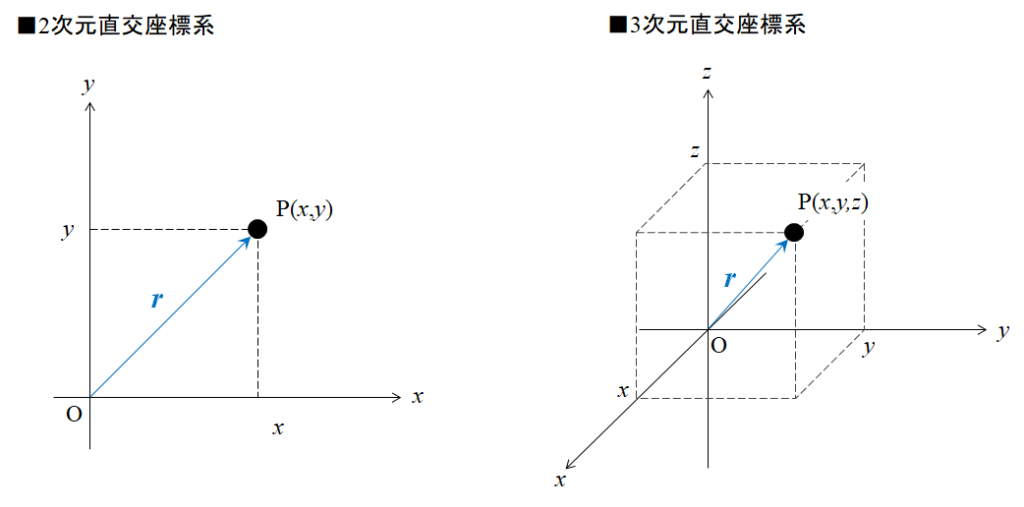
ベクトルと座標系を組みあわせて考えるために単位ベクトル\(\boldsymbol e\)を用います。
単位ベクトルとは大きさが1のベクトル(\(|\boldsymbol e|=1\))です。
これを2次元直交座標系の場合には原点から\(x\)軸方向と\(y\)軸方向に伸ばします。
原点から\(x\)軸方向、\(y\)軸方向に伸ばした単位ベクトルをそれぞれ\(\boldsymbol e_x\)、\(\boldsymbol e_y\)とします。
3次元直交座標の場合は原点から\(x\)軸方向、\(y\)軸方向、\(z\)軸方向に伸ばした単位ベクトルをそれぞれ\(\boldsymbol e_x\)、\(\boldsymbol e_y\)、\(\boldsymbol e_z\)とします。
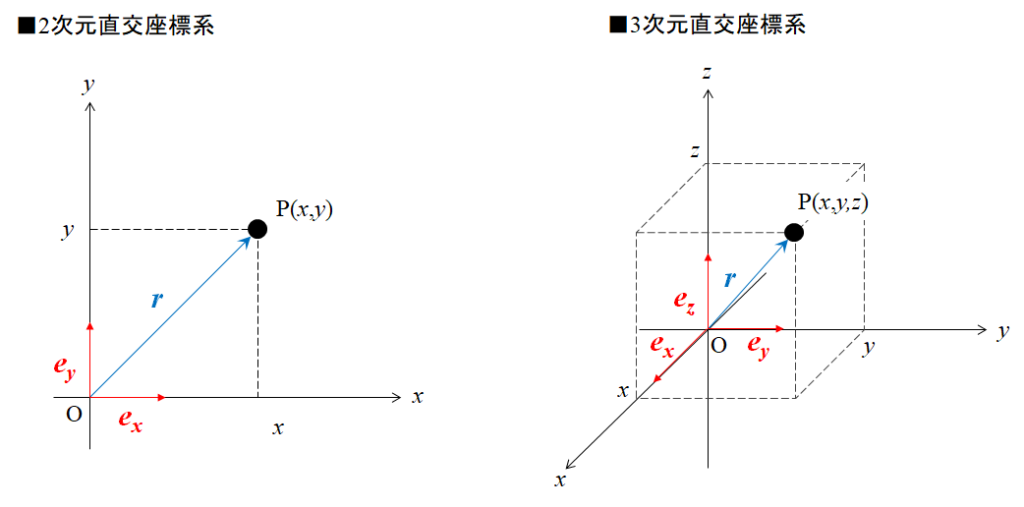
すると位置ベクトル\(\boldsymbol r\)は次のように表すことができます。
位置ベクトル\(\boldsymbol r\)
■2次元直交座標系
$$\boldsymbol r = x\boldsymbol e_x+y\boldsymbol e_y$$
■3次元直交座標系
$$\boldsymbol r = x\boldsymbol e_x+y\boldsymbol e_y+z\boldsymbol e_z $$
これは単位ベクトル\(\boldsymbol e_x \)、\(\boldsymbol e_y \)、\(\boldsymbol e_z \)がそれぞれ\(x\)、\(y\)、\(z\)方向を表しており、その前についている\(x\)、\(y\)、\(z\)が大きさを表しており、各成分を足し合わせているイメージです。
また\(\boldsymbol r\)の大きさ\(|\boldsymbol r|\)は三平方の定理を用いて導くことができます。
\(\boldsymbol r\)の大きさ\(|\boldsymbol r|\)
■2次元直交座標系
$$|\boldsymbol r|=\sqrt{x^2+y^2} $$
■3次元直交座標系
$$|\boldsymbol r|=\sqrt{x^2+y^2+z^2} $$
2次元・3次元空間の速度・加速度
続いて2次元・3次元空間における点の速度・加速度について考えていきます。
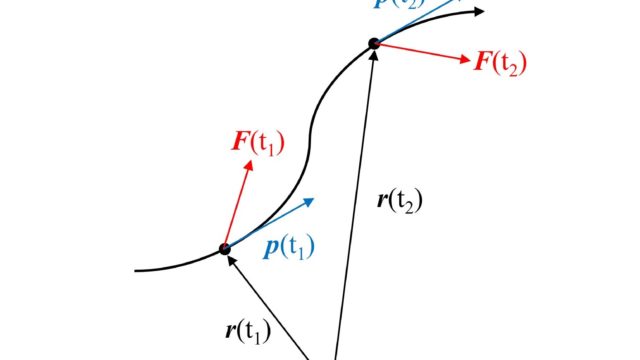
以前に1次元空間における速度・加速度については、時刻\(t\)における位置\(x(t)\)の時間微分が速度\(v(t)\)を表し、時刻\(t\)における速度\(v(t)\)の時間微分が加速度\(v(t)\)を表すことを説明しました。
2次元・3次元空間においても考え方は変わらず、位置ベクトルを時間微分することで速度が求まり、求まった速度を時間微分することで加速度を求めることができます。
まずは2次元空間における速度・加速度について見ていきましょう。
2次元空間における位置・速度・加速度
2次元空間における位置ベクトルは以下のように表されます。
$$\boldsymbol r = x\boldsymbol e_x+y\boldsymbol e_y$$
これを時間微分することによって速度\(\boldsymbol v= \frac{d\boldsymbol r}{dt} \)を求めることができます。
$$\frac{d\boldsymbol r}{dt} = \frac{dx}{dt}\boldsymbol e_x+\frac{dy}{dt}\boldsymbol e_y$$
さらに速度\(\boldsymbol v= \frac{d\boldsymbol r}{dt} \) を時間微分することによって加速度\(\boldsymbol a= \frac{d\boldsymbol v}{dt}=\frac{d^2\boldsymbol r}{dt^2} \)を求めることができます。
$$ \begin{align} \frac{d}{dt}(\frac{d\boldsymbol r}{dt})&=\frac{d}{dt}(\frac{dx}{dt}\boldsymbol e_x+\frac{dy}{dt}\boldsymbol e_y)\\\\ \frac{d^2\boldsymbol r}{dt^2}&= \frac{d^2x}{dt^2}\boldsymbol e_x+\frac{d^2y}{dt^2}\boldsymbol e_y \end{align} $$
以上で、2次元空間における位置・速度・加速度がわかったのでまとめておきます。
2次元空間における位置・速度・加速度
$$\begin{align}位置 \boldsymbol r &= x\boldsymbol e_x+y\boldsymbol e_y \\ \\速度 \boldsymbol v &= \frac{d\boldsymbol r}{dt} = \frac{dx}{dt}\boldsymbol e_x+\frac{dy}{dt}\boldsymbol e_y\\ \\加速度 \boldsymbol a &= \frac{d^2\boldsymbol r}{dt^2}= \frac{d^2x}{dt^2}\boldsymbol e_x+\frac{d^2y}{dt^2}\boldsymbol e_y \end{align} $$
3次元空間における位置・速度・加速度
続いて3次元空間における位置・速度・加速度について考えます。
位置ベクトルは以下のように表されます。
$$\boldsymbol r = x\boldsymbol e_x+y\boldsymbol e_y +z\boldsymbol e_z $$
これを時間微分することによって速度\(\boldsymbol v= \frac{d\boldsymbol r}{dt} \)を求めることができます。
$$\frac{d\boldsymbol r}{dt} = \frac{dx}{dt}\boldsymbol e_x+\frac{dy}{dt}\boldsymbol e_y +\frac{dz}{dt}\boldsymbol e_z $$
さらに速度\(\boldsymbol v= \frac{d\boldsymbol r}{dt} \) を時間微分することによって加速度\(\boldsymbol a= \frac{d\boldsymbol v}{dt}=\frac{d^2\boldsymbol r}{dt^2} \)を求めることができます。
$$ \begin{align} \frac{d}{dt}(\frac{d\boldsymbol r}{dt})&=\frac{d}{dt}(\frac{dx}{dt}\boldsymbol e_x+\frac{dy}{dt}\boldsymbol e_y +\frac{dz}{dt}\boldsymbol e_z)\\\\ \frac{d^2\boldsymbol r}{dt^2}&= \frac{d^2x}{dt^2}\boldsymbol e_x+\frac{d^2y}{dt^2}\boldsymbol e_y+\frac{d^2z}{dt^2}\boldsymbol e_z \end{align} $$
以上で、3次元空間における位置・速度・加速度がわかったのでまとめておきます。
3次元空間における位置・速度・加速度
$$\begin{align}位置 \boldsymbol r &= x\boldsymbol e_x+y\boldsymbol e_y +z\boldsymbol e_z \\ \\速度\boldsymbol v &= \frac{d\boldsymbol r}{dt} = \frac{dx}{dt}\boldsymbol e_x+\frac{dy}{dt}\boldsymbol e_y +\frac{dz}{dt}\boldsymbol e_z \\ \\ 加速度 \boldsymbol a &= \frac{d^2\boldsymbol r}{dt^2} = \frac{d^2x}{dt^2}\boldsymbol e_x+\frac{d^2y}{dt^2}\boldsymbol e_y+\frac{d^2z}{dt^2}\boldsymbol e_z \end{align} $$
おすすめの参考書
力学の理解のためにおすすめの参考書を3冊ほど紹介しておきます。
「考える力学」は丁寧に書かれており、初学者向けの参考書となっています。力学で用いる数学についても詳しく解説されており、力学を勉強する1冊目の本としておすすめです。
「基幹講座物理学 力学」は理工系では通常学ばないような発展的な内容が含まれているのが特徴です。大学1年生向けに執筆したようですが、自学用の1冊目としてはおすすめしません。2冊目や副読本としては良い選択肢でしょう。
「ファインマン物理学」は有名なシリーズですべて良書です。ファインマン博士の個性的な人柄が読み取れる参考書になっています。読者に対する話かけがあり、講義を受けているような感覚で読み進めることができます。
まとめ
2次元・3次元空間における位置・速度・加速度についてまとめておきましょう。
2次元空間における位置・速度・加速度
$$\begin{align}位置 \boldsymbol r &= x\boldsymbol e_x+y\boldsymbol e_y \\ \\速度 \boldsymbol v &= \frac{d\boldsymbol r}{dt} = \frac{dx}{dt}\boldsymbol e_x+\frac{dy}{dt}\boldsymbol e_y\\ \\加速度 \boldsymbol a &= \frac{d^2\boldsymbol r}{dt^2}= \frac{d^2x}{dt^2}\boldsymbol e_x+\frac{d^2y}{dt^2}\boldsymbol e_y \end{align} $$
3次元空間における位置・速度・加速度
$$\begin{align}位置 \boldsymbol r &= x\boldsymbol e_x+y\boldsymbol e_y +z\boldsymbol e_z \\ \\速度\boldsymbol v &= \frac{d\boldsymbol r}{dt} = \frac{dx}{dt}\boldsymbol e_x+\frac{dy}{dt}\boldsymbol e_y +\frac{dz}{dt}\boldsymbol e_z \\ \\ 加速度 \boldsymbol a &= \frac{d^2\boldsymbol r}{dt^2} = \frac{d^2x}{dt^2}\boldsymbol e_x+\frac{d^2y}{dt^2}\boldsymbol e_y+\frac{d^2z}{dt^2}\boldsymbol e_z \end{align} $$
1元空間における位置・速度・加速度の関係とどうように、2次元・3次元空間においても位置・速度・加速度は時間微分を行うことで計算することができます。
Baby steps to Giant strides !