今回はばね運動を題材にして単振動について考えていきます。
最近は落下運動を題材にして「落下運動・放物運動」「速度に比例する抵抗がある場合の落下運動」「速度の2乗に比例する抵抗がある場合の落下運動」について考えてきました。
今回はこれまでの落下運動とは打って変わってばね運動について考えていきます。
まずはばねの特性について考えます。
その後、運動方程式を立てて、微分方程式を解いていきます。
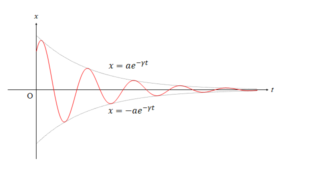
最後に運動の様子をグラフ化して、どのような運動をしているかを理解していきます。
ばね運動の単振動
なめらかで摩擦のない水平面に置かれた質量 $m$ のおもりに、ばねがついているとします。
ばねの他端は固定されているとします。
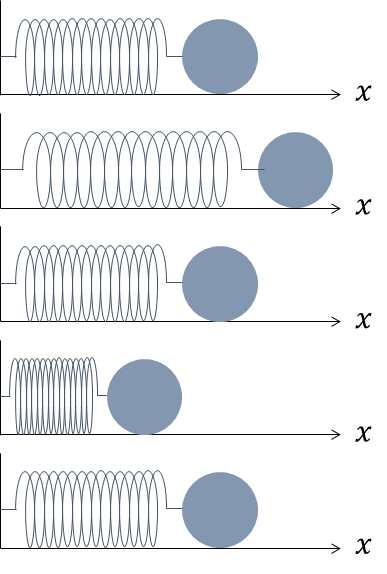
このときおもりを引っ張ってばねを伸ばした後に手を離すと、ばねは伸び縮みしておもりは振動し始めます。
今は摩擦がない場合について考えているので、おもりは振動し続けます。
このとき、おもりの位置 $x$ はどのような変化をするのか?が問題になります。
おもりの運動を考えていくので、運動方程式を立てるためにまずはおもりにかかる力について考えていきます。
おもりの振動方向の力はばねから加えられます。
そこで、ばねを伸ばしたり縮めたりするときにどのように、ばねからおもりにどのように力が加えられるかについて考えましょう。
ばねの伸び縮みがない場合、つまりばねの長さが自然長の場合、力は0になります。
ばねが自然長から伸びている場合、伸びた長さに比例した力が、伸びた方向とは逆方向に加わります。
ばねが自然長から縮んでいる場合、縮んだ長さに比例した力が、縮んだ方向とは逆方向に加わります。
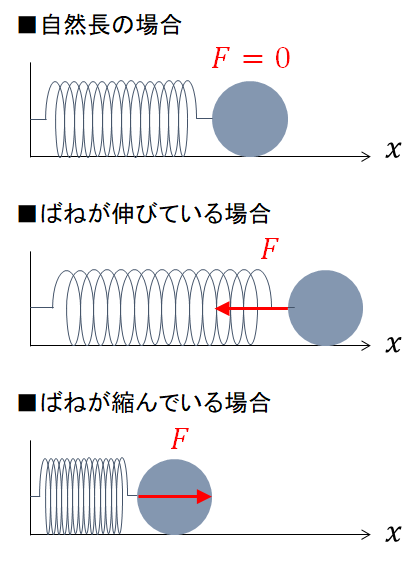
ばねにはこのような性質があり、フックの法則と言います。
ばねからおもりに加わる力を $F$ とし、ばねが自然長のときのおもりの位置を $x=0$ 、時刻 $t$ のときのおもりの位置を $x(t)$ とします。 初期条件は位置 $x(t=0)=x_0$、速度 $v(t=0)=\frac{dx(t=0)}{dt}=0$ とします。
すると比例定数 $k>0$ を用いてフックの法則は次のように表せます。
$$
\begin{align}
F(t)=-kx(t)
\end{align}
$$
この比例定数 $k$ はばね定数と呼ばれます。符号にマイナスがついていますが、これはおもりに加わる力がばねの伸び縮みに対して逆方向に加わることを表しています。
これで、ばねからおもりに加わる力がわかったので運動方程式は、
$$
\begin{align}
m\frac{d^2x(t)}{dt^2}=-kx(t)
\end{align}
$$
となります。両辺を $m$ で割ると、
$$
\begin{align}
\frac{d^2x(t)}{dt^2}=-\frac{k}{m}x(t)
\end{align}
$$
になります。式を見やすくするために $\frac{k}{m}$ を $\omega^2$ とおきます。すると、
$$
\begin{align}
\frac{d^2x(t)}{dt^2}=-\omega^2x(t)
\end{align}
$$
となります。さて次はこの2階線形微分方程式を解いていくことになります。
これまで微分方程式は変数分離法を用いて階を求めてきましたが、それでは2階線形微分方程式を解けません。
そこで、解となる関数を当てはめていき、一般解を考えていきます。
この微分方程式をみると、$t$ で2回微分すると元の式に $-\omega^2$ かけた式になるような関数 $x(t)$ を求めることになります。
このような微分方程式の解は三角関数 $\sin$ や $\cos$ がでてくることが想像できそうですよね。
まず、$x(t)$ を $\cos$ を用いて、
$$
\begin{align}
x(t)=\cos \omega t
\end{align}
$$
とおきます。これを2回微分すると、
$$
\begin{align}
\frac{dx(t)}{dt}&=-\omega\sin \omega t\\
\\
\frac{d^2x(t)}{dt^2}&=-\omega^2\cos \omega t=-\omega^2x(t)
\end{align}
$$
となります。つまり $x(t)=\cos\omega t$ は1つの解となることがわかります。
同様にして$x(t)$ を $\sin$ を用いて、
$$
\begin{align}
x(t)=\sin \omega t
\end{align}
$$
とおきます。これを2回微分すると、
$$
\begin{align}
\frac{dx(t)}{dt}&=\omega\cos \omega t\\
\\
\frac{d^2x(t)}{dt^2}&=-\omega^2\sin \omega t=-\omega^2x(t)
\end{align}
$$
となります。つまり $x(t)=\sin\omega t$ は1つの解となることがわかります。
線形微分方程式の一般解は独立な解の線形結合で書けます。
$\sin\omega t$ と $\cos\omega t$ は線形独立なので、この微分方程式の一般解は定数 $A,B$ を用いて
$$
\begin{align}
x(t)=A\sin \omega t+B\cos \omega t
\end{align}
$$
と書けます。また、速度は両辺を微分して
$$
\begin{align}
v(t)=\frac{dx(t)}{dt}=A\omega\cos \omega t-B\omega\sin \omega t
\end{align}
$$
となります。後は初期条件を代入して、運動の様子を確認していきましょう。
初期条件は位置 $x(t=0)=x_0$、速度 $v(t=0)=\frac{dx(t=0)}{dt}=0$ なので代入していきます。
まず $x(t=0)=x_0$ を代入していくと
$$
\begin{align}
A\sin (\omega \cdot 0) +B\cos (\omega \cdot 0)=x_0\\
A\sin 0+B\cos 0=x_0\\
B=x_0\
\end{align}
$$
となります。続いて $\frac{dx(t=0)}{dt}=0$ を代入していくと、
$$
\begin{align}
A\omega\cos (\omega \cdot 0) -B\omega\sin (\omega \cdot 0)=0\\
A\omega\cos 0-B\omega\sin 0=0\\
A=0
\end{align}
$$
となります。よって、位置 $x(t)$ と速度 $v(t)$ は、
$$
\begin{align}
x(t)&=x_0\cos \omega t\\
\\
v(t)&=\frac{dx(t)}{dt}=-x_0\omega\sin \omega t
\end{align}
$$
となります。ばね運動の位置は $\sin$ や $\cos$ といった三角関数を用いて振動を表すことができました。このような振動のことを単振動または調和振動といいます。
それではこの運動の様子をグラフ化してみていきましょう。
$$
\begin{align}
x(t)&=x_0\cos \omega t
\end{align}
$$
なので、振幅 : $x_0$、周期 : $T=2\pi/\omega$ となります。
また、 $\omega$ : 角振動数といいます。
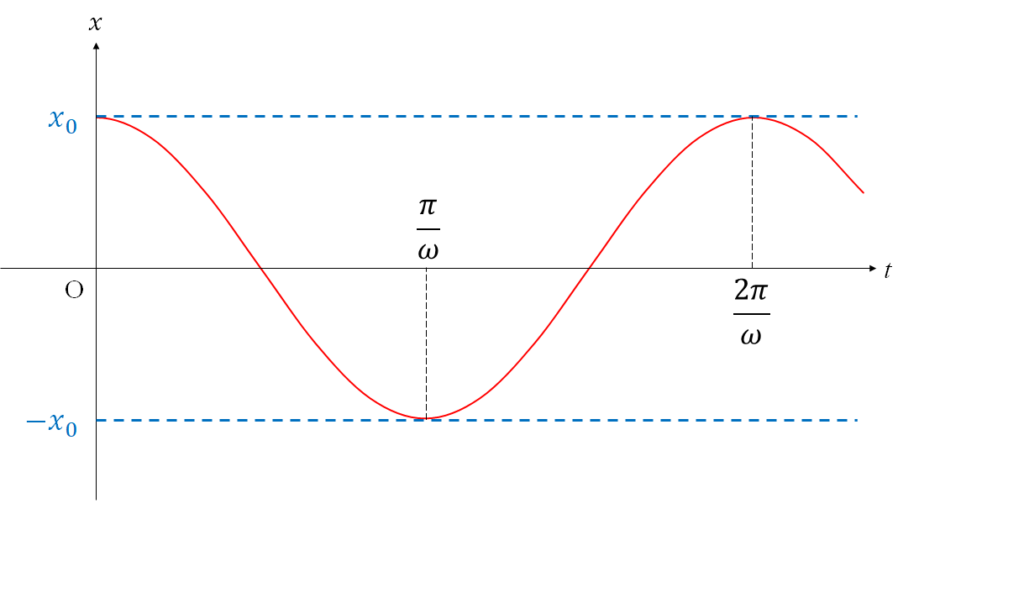
よってこのばねの運動は、初期条件のばねが伸びた状態である $x=x_0$ の位置から運動をスタートして、ばねが縮む方向におもりは移動していきます。
そして、 おもりが移動してばねが縮んだ状態になり$x=-x_0$ の位置まで移動したら、今度はおもりがばねの伸びる方向へ移動し、 $x=x_0$ の位置まで移動すると再び、ばねが縮む方向に移動していきます。
最初の位置 $x=x_0$ から運動を開始し、ふたたび位置 $x=x_0$ に戻ってくるまでの時間が1周期、すなわち $T=2\pi/\omega$ となります。
速度 $v$ は
$$
\begin{align}
v(t)&=-x_0\omega\sin \omega t
\end{align}
$$
なので、振幅 : $x_0\omega$、周期 : $T=2\pi/\omega$ となります。
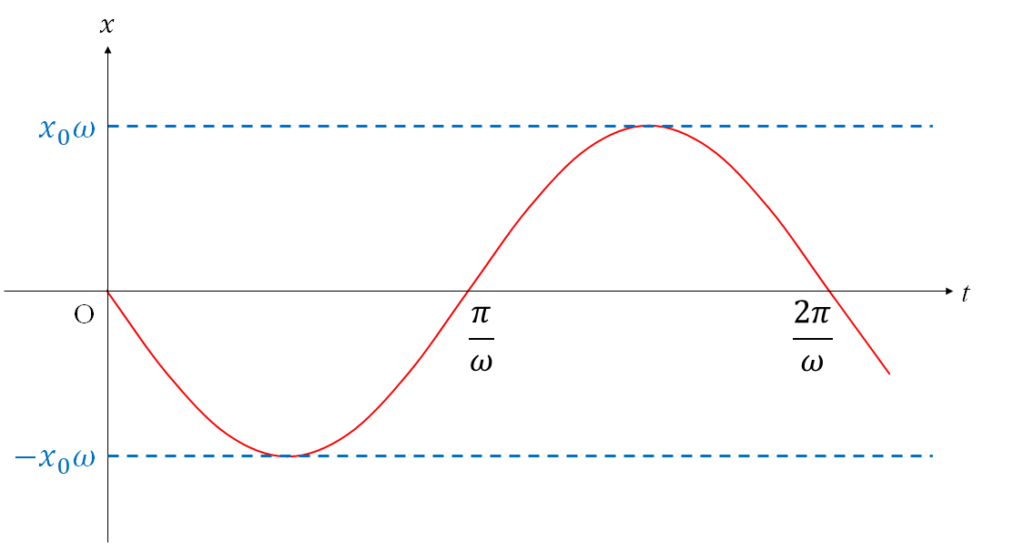
このグラフをみてわかるように、速度は、ばねが伸び切ったり、縮み切ったりしている位置 $x=x_0,-x_0$ では速度がゼロになります。
そして速度の大きさが最大になるのは $x=0$ のとき、すなわちばねが自然長になる位置で速度の大きさが最大となります。
最後に
今回は単振動について考えました。
運動方程式を立てているときに
$$
\begin{align}
\frac{d^2x(t)}{dt^2}=-\omega^2x(t)
\end{align}
$$
のような2階線形微分方程式の形になったときには単振動となります。
2階線形微分方程式では変数分離では上手く計算できないので注意しましょう。
微分方程式の解き方については一足飛びに一般解が出てきています。
これは単振動の運動について考えているのに、微分方程式の解き方を詳しく書いていると数学の話になってしまうと感じたからです。
そのうち微分方程式の解き方について補足していこうと思います。
Baby steps to Giant strides !