【物理】運動量と力積/運動量保存則【力学】

今回は「運動量と力積の関係」と「運動量保存則」について考えていきます。

運動の様子を考えるとき、ニュートンの第2法則にある運動方程式を用いますが、この運動方程式を式変形することで運動量と力積の関係や運動量保存則を導くことができます。

【物理】運動方程式(落下運動・放物運動)【力学】
↑ニュートンの法則についても書いています。

保存量とは運動を経ても変化しない量のことであり、外部から力を受けない系の運動では運動量が保存します。

今回の記事では、

運動量の定義
運動量と力積の関係
運動量保存則の導出

について解説していきます。

運動量と力積

まずは運動量と力積の関係について考えます。

質点の質量$m$に速度$\boldsymbol v=\frac{d\boldsymbol{r}}{dt}$をかけたベクトル量で定義される「運動量」と呼ばれる量

\begin{eqnarray}
\boldsymbol{p}=m\boldsymbol{v}\tag{1}
\end{eqnarray}

を定義します。この式の両辺を$t$で微分すると、

\begin{eqnarray}
\frac{d\boldsymbol{p}}{dt}&=&m\frac{d\boldsymbol{v}}{dt}\\
&=&m\frac{d^2\boldsymbol{r}}{dt^2}\tag{2}
\end{eqnarray}

となります。ここで、運動方程式を運動量$\boldsymbol{p}$を用いて表すと、

\begin{eqnarray}
\boldsymbol{F}&=&m\frac{d^2\boldsymbol{r}}{dt^2}\\
&=&\frac{d\boldsymbol{p}}{dt}\tag{3}
\end{eqnarray}

となります。この式から質点の運動量の時間微分はその瞬間にはたらく力に等しいことがわかります。さて、ここからは時刻$t_1$から$t_2$までの質点の運動について考えていきます。時刻$t$における位置ベクトルを$\boldsymbol{r}(t)$、運動量を$\boldsymbol{p}(t)$とします。

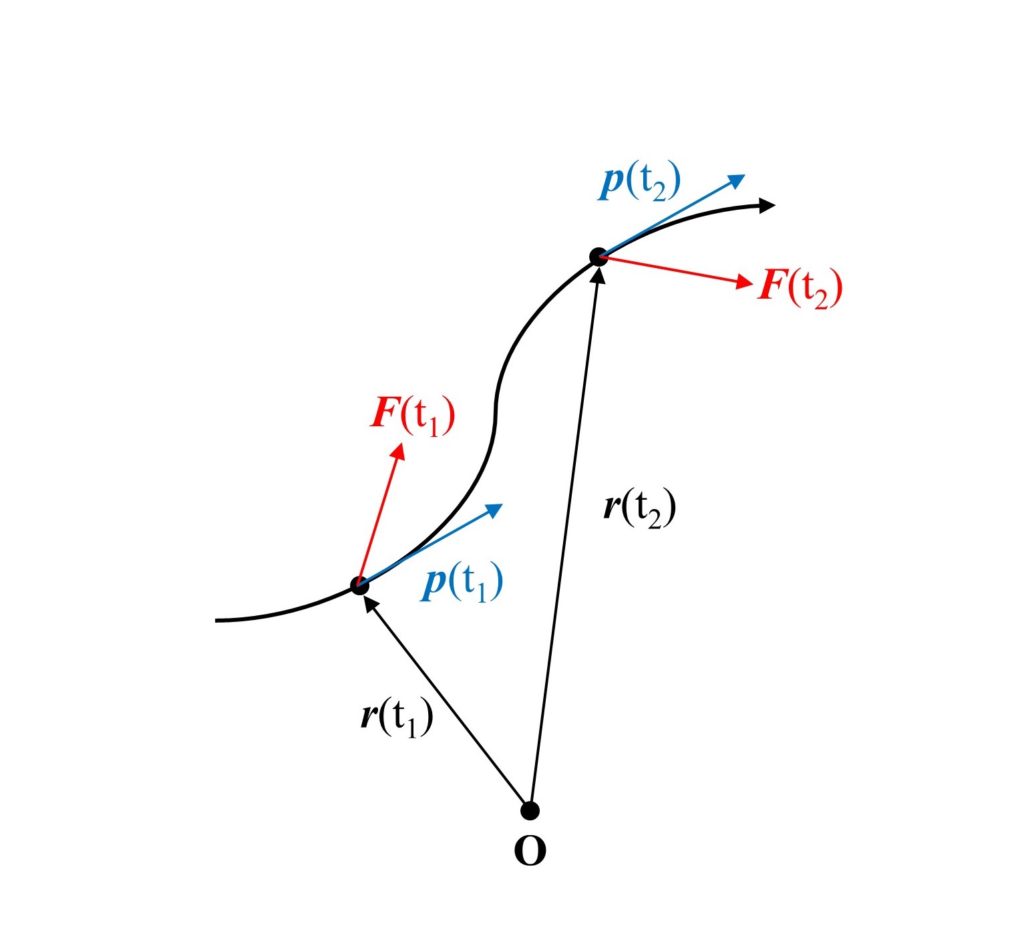
式(3)の両辺を時刻$t$に関して$t_1$から$t_2$まで積分すると、

\begin{eqnarray}
\int_{t_1}^{t_2}\boldsymbol{F}dt&=&\int_{\boldsymbol p(t_1)}^{\boldsymbol p(t_2)}d\boldsymbol{p}\\
&=&\boldsymbol p(t_2)-\boldsymbol p(t_1)\tag{4}
\end{eqnarray}

となります。式(4)の左辺は力$\boldsymbol{F}$の$t_1$から$t_2$までの力積といいます。

力積は$\boldsymbol I$を用いて表すことが多いです(Inpulseなので）。

\begin{eqnarray}
力積：\boldsymbol I&=&\int_{t_1}^{t_2}\boldsymbol{F}dt\tag{5}
\end{eqnarray}

よって、力積と運動量の関係は

\begin{eqnarray}
\boldsymbol I&=&\boldsymbol p(t_2)-\boldsymbol p(t_1)\tag{6}
\end{eqnarray}

となります。

運動量保存則

続いては運動量保存則を導きます。例として、2個の質点(質点1、質点2)が相互作用のみで運動している場合を考えます。

質点1,2の質量を$m_1,m_2$とし、位置$\boldsymbol{r}_1(t),\boldsymbol{r}_2(t)$とします。

また、受けている力を$\boldsymbol{F}_{12}(t),\boldsymbol{F}_{21}(t)$とし、運動量を$\boldsymbol{p}_1(t),\boldsymbol{p}_2(t)$とします。

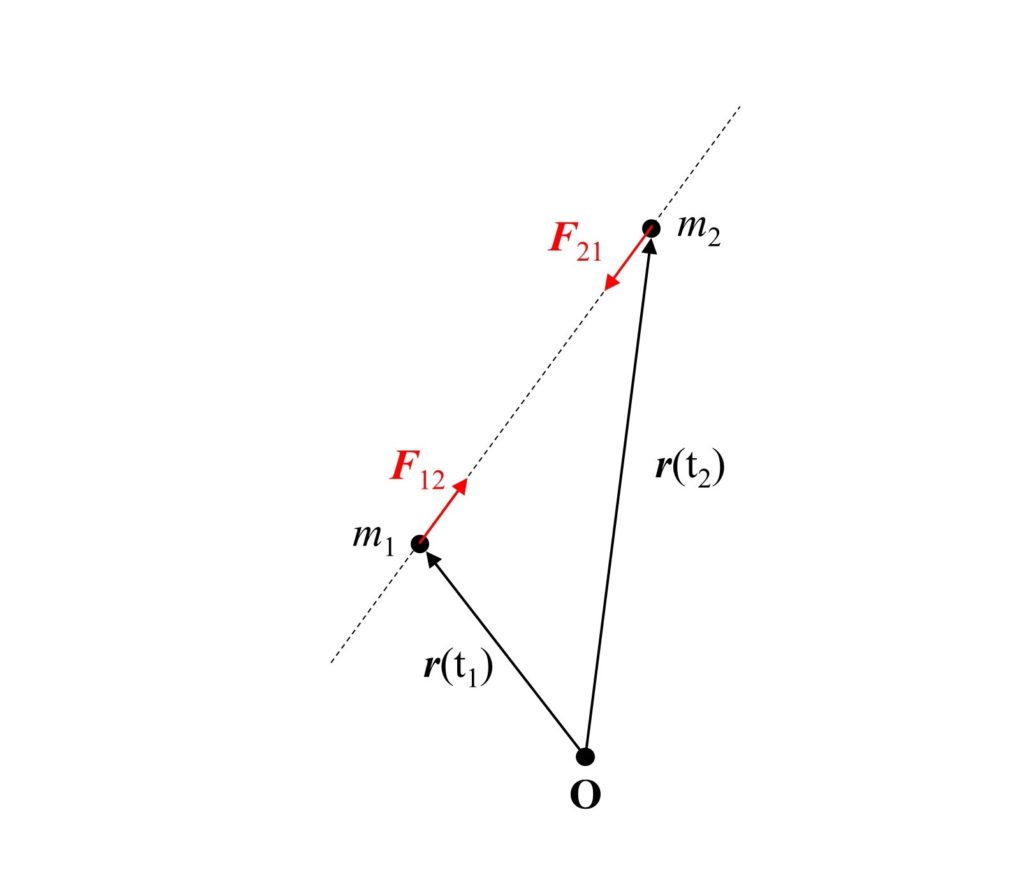
いま2個の質点には相互作用のみがはたらいているので、ニュートンの第3法則(作用・反作用の法則)より

\begin{eqnarray}
\boldsymbol{F}_{12}(t)=-\boldsymbol{F}_{21}(t)\equiv\boldsymbol{F}(t)\tag{7}
\end{eqnarray}

となります。時刻$t_1$から$t_2$までの運動を考えることにします。

このとき質点1の運動量と力積の関係(式(4))により、

\begin{eqnarray}
\int_{t_1}^{t_2}\boldsymbol{F}_{12}(t)dt&=&\boldsymbol p_1(t_2)-\boldsymbol p_1(t_1)\\
\int_{t_1}^{t_2}\boldsymbol{F}(t)dt&=&\boldsymbol p_1(t_2)-\boldsymbol p_1(t_1)\tag{8}
\end{eqnarray}

となります。同様に質点2の運動量と力積の関係により、

\begin{eqnarray}
\int_{t_1}^{t_2}\boldsymbol{F}_{21}(t)dt&=&\boldsymbol p_2(t_2)-\boldsymbol p_2(t_1)\\
-\int_{t_1}^{t_2}\boldsymbol{F}(t)dt&=&\boldsymbol p_2(t_2)-\boldsymbol p_2(t_1)\tag{9}
\end{eqnarray}

となります。式(8)(9)より、

\begin{eqnarray}
-(\boldsymbol p_1(t_2)-\boldsymbol p_1(t_1))&=&\boldsymbol p_2(t_2)-\boldsymbol p_2(t_1)\\
\boldsymbol p_1(t_1)+\boldsymbol p_2(t_1)&=&\boldsymbol p_1(t_2)+\boldsymbol p_2(t_2)\tag{10}
\end{eqnarray}

式(10)の左辺は時刻$t_1$の全運動量となっており、式(10)の右辺は時刻$t_2$の全運動量となっています。

このことから相互作用によって質点1,2それぞれの運動量$\boldsymbol p_1(t),\boldsymbol p_2(t)$は変化しますが、全運動量は時刻が変化しても一定に保たれることがわかります。

これを2質点の系の「運動量保存則」といいます。