どのようにすれば効率的ポートフォリオを構築できるかについて考えていきます。
インデックス投資に限らず、長期投資をする場合には「どのような資産配分で投資をしていけばよいのか?」という疑問を持ったことはありませんか?
インデックス投資では資産配分のおすすめとして
- 1.世界各国の時価総額と同じ比率で資産配分方法
- 2.期待収益率やボラティリティ(リスク)、相関から最も効率的な組み合わせを計算して資産配分する方法
があげられることが多いです。
今回は2.について2銘柄というシンプルな状況で期待収益率とボラティリティの関係性について見ることでどのようにすれば効率的なポートフォリオを組むことができるのかについて考えていきます!
2銘柄による収益率とボラティリティ
シンプルに2銘柄でどのようにすれば効率的ポートフォリオを構築できるかについて考えていきます。
仮想のA社・B社について以下の表のように期待収益率とボラティリティ(リスク)を準備します。

今回、このA社とB社については無相関 (相関係数0) とします。
ここで一例としてA社に40%、B社に60%投資したポートフォリオについて考えてみます。
\(期待収益率=0.40×25\%+0.60×5\%=13\%\)
\(ボラティリティ=\sqrt{(0.4×0.5)^2+(0.6×0.25)^2}×100=25.0\%\)
となります。
これと同様に、A社とB社に対して様々なポートフォリオウェイト(A社とB社への投資比率)で期待収益率とボラティリティを計算していきます。
以下の表に主要なポートフォリオで計算した期待収益率とボラティリティを示します。
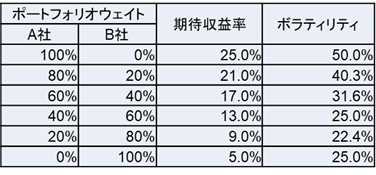
表を見ればわかりますが、2社の銘柄を組み合わせてポートフォリオを調整することで期待収益率とボラティリティを変化させることができます。
これによって自分にとって最適な期待収益率とボラティリティを選択することができます。
効率的ポートフォリオと非効率的ポートフォリオ
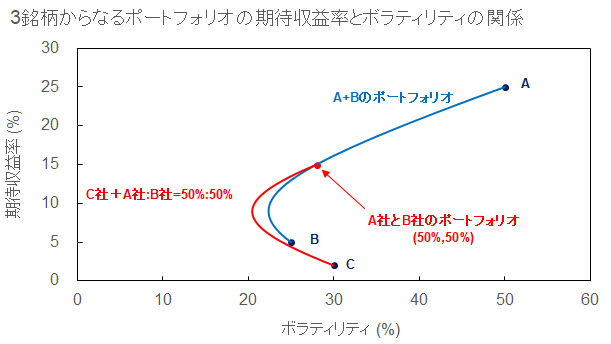
上の表で、主要なポートフォリオの期待収益率とボラティリティの計算結果を示しましたが、下図に2銘柄からなるポートフォリオの期待収益率とボラティリティの関係を示します。
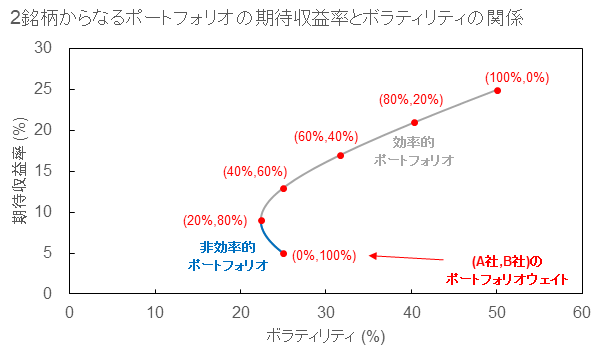
表中の曲線がA社・B社の株式を任意のポートフォリオで組み合わせたときの期待収益率とボラティリティの関係を示しており、赤い点が上表で示した主要なポートフォリオの期待収益率とボラティリティになっています。
曲線の灰色部分が効率的ポートフォリオ、青色部分が非効率的ポートフォリオと呼ばれます。
なぜ青い曲線部分を非効率的ポートフォリオと呼ぶかというと、別のポートフォリオによって期待収益率とボラティリティを共に改善することができるからです。
例えばA社、B社のポートフォリオが(0%,100%)のときと(30%,70%)のときの期待収益率とボラティリティを比較して見ましょう。
(A社,B社)= (0%,100%)のとき
- 期待収益率・・・5%
- ボラティリティ・・・25.0%
(A社,B社)= (30%,70%)のとき
- 期待収益率・・・11%
- ボラティリティ・・・23.0%
一目瞭然だと思いますが、ポートフォリオを(A社,B社)= (0%,100%)→(A社,B社)= (30%,70%)にすると、期待収益率が5%→11%、ボラティリティが25.0%→23.0%と共に改善されています。
このように曲線の青い部分については別のポートフォリオによって期待収益率とボラティリティを共に改善することができるので、非効率的ポートフォリオと呼ばれます。
もし投資していてポートフォリオを組むときに期待収益率とボラティリティについて計算してみようと思った場合には、自分のポートフォリオが非効率的ポートフォリオになっていないかどうかはチェックしてみて良いかもしれませんね。
ポートフォリオを見直すべきかどうかを判断することができます。
一方で自分のポートフォリオが効率的ポートフォリオであった場合には、一概にどのポートフォリオがベストとは言えません。
効率的ポートフォリオにおいては期待収益率を上げようとすればボラティリティも上がるというように利益とリスクがトレードオフの関係になっています。
なので各々が自分に適した期待収益率とボラティリティを選択して投資していく必要があります。
例えばある程度リスクをとってでも利益を増やしたいと考えている人はA社の比率を高くしたポートフォリオを組むことになりますし、利益が減ってでもリスクを下げたいと考える人はB社の比率を高くしたポートフォリオを組むことになるでしょう。
最後に
今回は2銘柄というシンプルな状況を仮定してポートフォリオの期待収益率とボラティリティの関係を見ていきました。
2銘柄のあらゆるポートフォリオで期待収益率とボラティリティを計算することで、それらの関係性を見ることができます。
非効率的ポートフォリオを避けて効率的ポートフォリオになる範囲で銘柄を組み合わせることで、計算上効率的な投資をすることができます。
今回は相関0として計算をおこないましたが、実際には銘柄ごとの相関がボラティリティ(リスク)に影響してきます。この辺りは後々追記していこうと考えています。
Baby steps to Giant strides !