ポートフォリオのリスクを知るためには、株式の収益率とリスクを知るだけではいけません。
ポートフォリオを構成する株式が直面する共通リスクの大きさとその連動度合いを知る必要があります。
これらを知るために重宝されるのが共分散と相関です。
共分散と相関を利用することで、収益率間の連動性を知ることができます。
今回は収益率の共分散と相関を計算しながら求めていきます。
共分散を求めてみる
共分散は2つの収益率の平均からの乖離の積の期待値のことです。
何を言っているのかわかりにくいですよね。
具体例を出して計算しながら見ていきましょう。
前回使用したこちらの収益率の値を使いまわしていこうと思います。
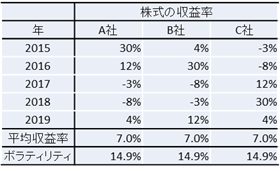
先ほど、共分散は2つの収益率の平均からの乖離の積の期待値といいました。
だから、共分散を求めるにはまず収益率の平均値からの乖離を調べる必要があります。
ようするに、(各年度の収益率)―(平均収益率)を計算しろってことです。
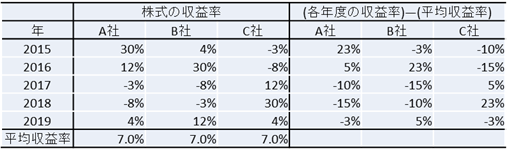
続いて、共分散は2つの収益率の平均からの乖離の積の期待値ですので、2つの収益率の平均からの乖離の積を求めていきます。
これはA社とB社の共分散を求めたければ、この2社の(各年度の収益率)―(平均収益率)を掛け算すればいいだけです。
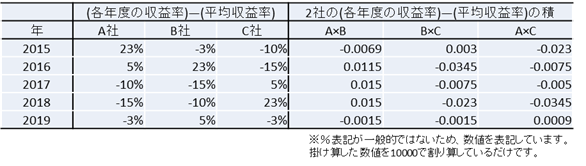
最後にこれらの期待値を求めれば共分散の値を得られます。
期待値は2社の(各年度の収益率)―(平均収益率)の積をすべてたして(足した数)―1で割り算すれば求まります。
ややこしいですが実際に計算してみれば簡単です。A社とB社で見てみましょう。
まず、A社とB社の(各年度の収益率)―(平均収益率)の積をすべて足します。
-0.0069+0.0115+0.015+0.015+(-0.0015)=0.0331
これを(足した数)―1で割ります。足した値の数は5年分なので5。
なので5-1=4で割ります。
0.0331÷4=0.008275
となります。これで共分散が求まりました。
なぜ、ここで(足した数)―1で割り算するんだ?と思う人もいるかもしれませんが、ここではそこは一旦無視してください。説明するとややこしいので。
残りのB社とC社、A社とC社の共分散も計算すると次のようになります。
- A社とB社の共分散・・・0.008275
- B社とC社の共分散・・・-0.015875
- A社とC社の共分散・・・-0.017275
これで共分散が求まりました。
共分散で注目するべきは符号です。
- 共分散が正の値・・・2つの株式の収益率の増減方向が同じ
- 共分散が負の値・・・2つの株式の収益率の増減方向が逆
A社とB社の共分散は正の値ですが、A社の収益率が平均より増加すると、B社の収益率も平均より増加する傾向にあり、A社の収益率が平均より減少すると、B社の収率も平均より減少する傾向にあるということです。
B社とC社の共分散は負の値ですが、B社の収益率が平均より増加すると、C社の収益率は平均より減少する傾向にあり、B社の収益率が平均より減少すると、C社の収益率は平均より増加する傾向にあるということです。
このことからわかるように共分散を求めることで2社の株式収益率の関係性を知ることができます。
ただし、共分散だけでは関連度合いがわかりません。
一見、共分散の数字部分が関連度合いの強さを表しているのではないか?と思ってしまいそうですが、変化の大きさを示しているだけです。関連度合いの大きさは示していません。
そこで、関連度合の大きさを知るために重要なのが相関です。
相関を求めてみる
2つの株式の相関を求めるには、先ほど求めた2社の共分散の2社のボラリティで割ることで求めることができます。
今、A,B,C社のボラリティは0.149(14.9%)になっています。
なのでA社とB社の相関は
0.008275÷0.149÷0.149=0.373
となります。
同様にしてB社とC社の相関を求めると-0.715となります。
相関は常にー1と1の間の値になります。
だから、2つの株式間の関係の強さを正しく評価できます。
- 相関が1に近い・・・収益率が同じ方向に動きやすい
- 相関が0に近い・・・収益率の関係性はほとんどない
- 相関がー1に近い・・・収益率が反対方向に動きやすい
先ほど求めたA社とB社の相関は0.373となっていましたが、これをどのように解釈できるかというと、A社の収益率が増えるとB社の収益率も増える傾向があるが、その関連性はそれほど強くないといったところでしょうか。
B社とC社の相関は-0.713となっていましたが、これはB社の収益率が増えるとC社の収益率が減る傾向にあり、その関連性はかなり強いということです。
計算がめんどくさいと思った人は多いと思いますが、相関はEXCELでCORREL関数を使うと簡単に計算できます。
相関については理解したから簡単に計算できるようにしたいという人はEXCELを大いに利用してください。
個別株で長期投資をする場合は相関関係を分析して購入すべき
相関関係を把握するのは、投資信託を購入するときよりも個別株で長期投資をしようとする場合に大きな力を発揮すると僕は思います。
投資信託は1銘柄でも数百社など多くの株式に分散投資されているのが普通なので、相関を調べずとも十分に分散されて投資できていることが普通です。
一方、個別投資で長期投資をやろうとした場合、一般人には数百社に分散投資は不可能です。
多くてもせいぜい数十社でしょう。
個別投資で購入銘柄が少ない場合、効率的にリスクを下げる必要があります。
適当に複数の個別株を購入して分散したつもりになっていても、思ったほどリスクが下がっていない可能性は大いにあり得ます。
だからこそ、相関関係を調べるのは非常に効果的な手段といえるでしょう。
最後に
共分散と相関から収益率間の連動性がわかることを確認しました。
2社の株式の相関から以下の傾向があることを確認できます。
- 相関が1に近い・・・収益率が同じ方向に動きやすい
- 相関が0に近い・・・収益率の関係性はほとんどない
- 相関がー1に近い・・・収益率が反対方向に動きやすい
相関はEXCELでCORREL関数を使うと簡単に計算できます。
個別投資で長期投資をしようと考えている人にとっては重要なファクターと言えるでしょう。